Question Number 174191 by Best1 last updated on 26/Jul/22
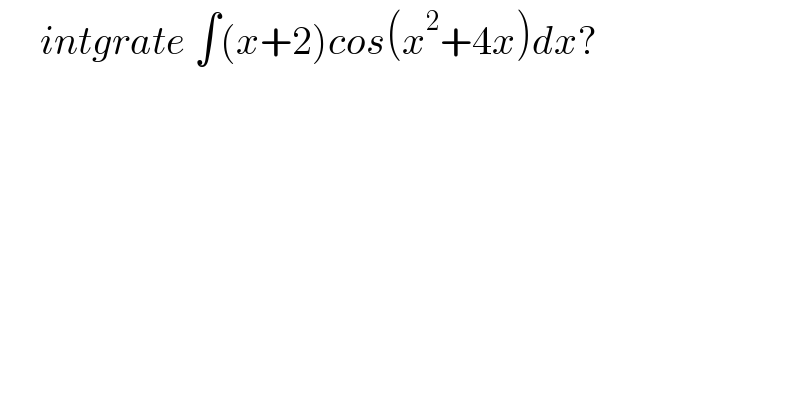
$$\:\:\:\:\:{intgrate}\:\int\left({x}+\mathrm{2}\right){cos}\left({x}^{\mathrm{2}} +\mathrm{4}{x}\right){dx}? \\ $$
Commented by mokys last updated on 26/Jul/22
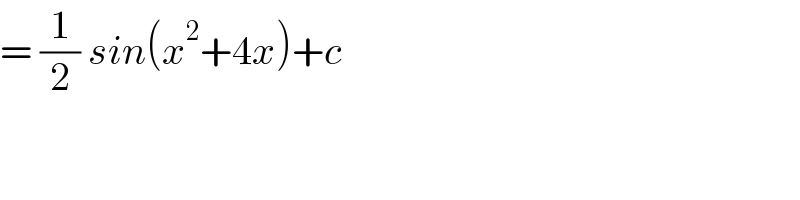
$$=\:\frac{\mathrm{1}}{\mathrm{2}}\:{sin}\left({x}^{\mathrm{2}} +\mathrm{4}{x}\right)+{c} \\ $$
Commented by MJS_new last updated on 27/Jul/22
![∫(x+2)cos (x^2 +4x) dx= [t=x^2 +4x → dx=(dt/(2x+4))] =(1/2)∫cos t dt](https://www.tinkutara.com/question/Q174219.png)
$$\int\left({x}+\mathrm{2}\right)\mathrm{cos}\:\left({x}^{\mathrm{2}} +\mathrm{4}{x}\right)\:{dx}= \\ $$$$\:\:\:\:\:\left[{t}={x}^{\mathrm{2}} +\mathrm{4}{x}\:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{2}{x}+\mathrm{4}}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{cos}\:{t}\:{dt} \\ $$
Commented by Best1 last updated on 27/Jul/22

$${how}\:??{show}\:{me}\:{steps} \\ $$
