Menu Close

let-f-a-0-1-e-t-ln-1-e-at-dt-with-a-0-1-find-f-a-2-calculate-f-a-3-find-the-value-of-0-1-e-t-ln-1-e-3t-dt-

Tinku Tara 0 Comments
Pin




Question Number 36755 by prof Abdo imad last updated on 05/Jun/18
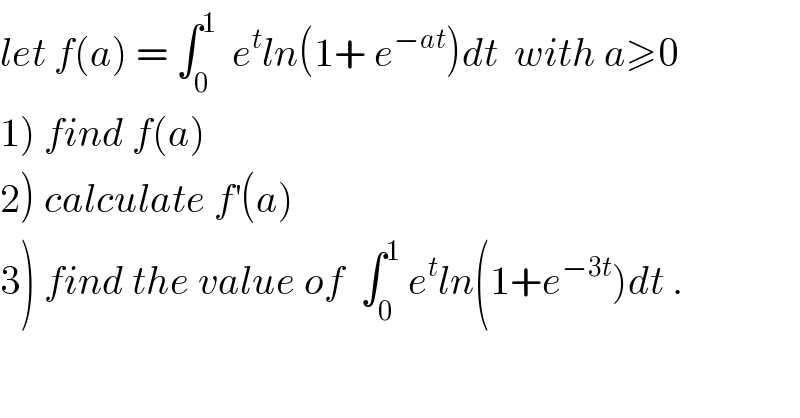
let f(a) = ∫_0 ^1 e^t ln(1+ e^(−at) )dt with a≥0 1) find f(a) 2) calculate f^′ (a) 3) find the value of ∫_0 ^1 e^t ln(1+e^(−3t) )dt .
$${let}\:{f}\left({a}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{e}^{{t}} {ln}\left(\mathrm{1}+\:{e}^{−{at}} \right){dt}\:\:{with}\:{a}\geqslant\mathrm{0} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{f}\left({a}\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:{f}^{'} \left({a}\right) \\ $$$$\left.\mathrm{3}\right)\:{find}\:{the}\:{value}\:{of}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{{t}} {ln}\left(\mathrm{1}+{e}^{−\mathrm{3}{t}} \right){dt}\:. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 05/Jun/18
Commented by abdo.msup.com last updated on 05/Jun/18
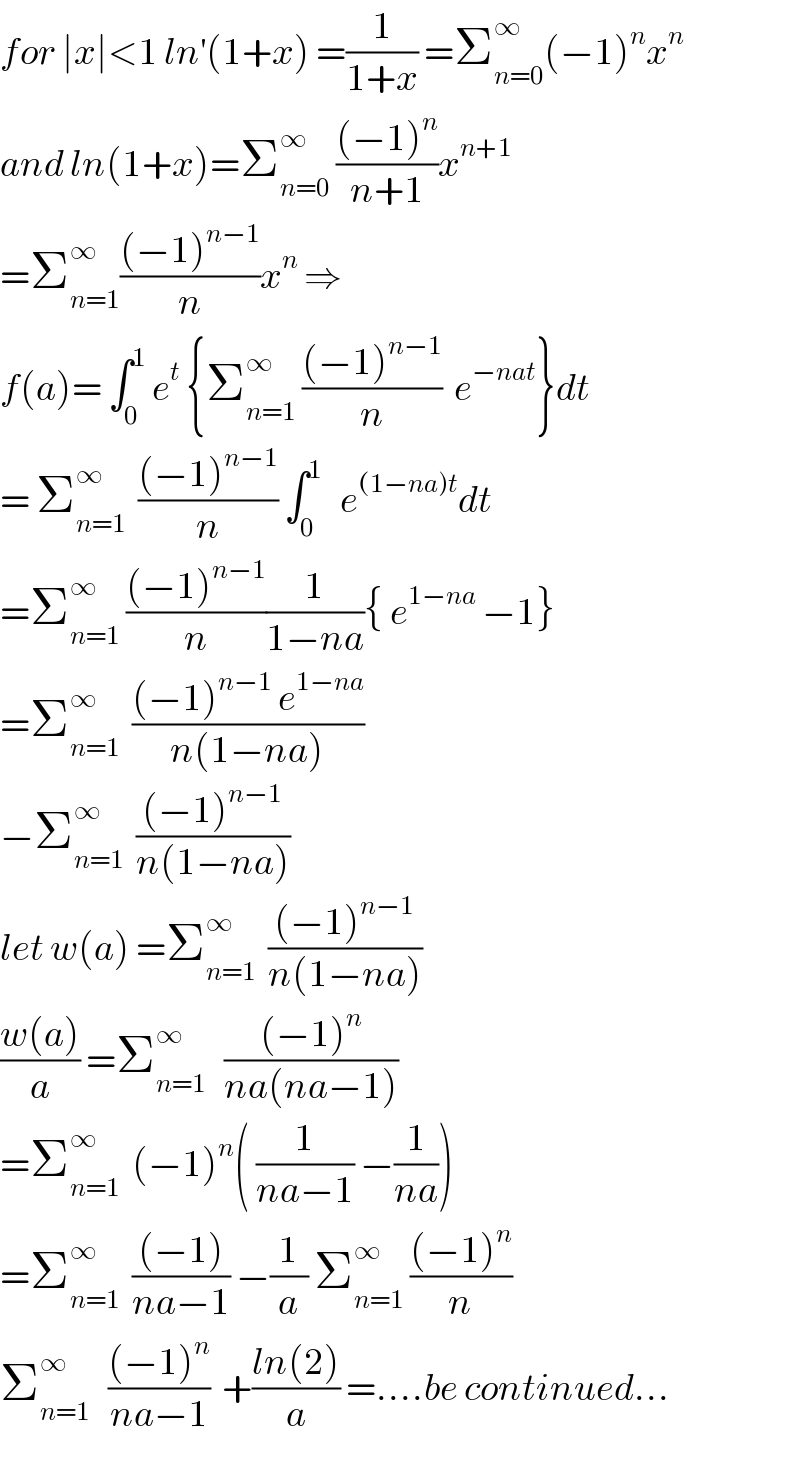
for ∣x∣<1 ln^′ (1+x) =(1/(1+x)) =Σ_(n=0) ^∞ (−1)^n x^n and ln(1+x)=Σ_(n=0) ^∞ (((−1)^n )/(n+1))x^(n+1) =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)x^n ⇒ f(a)= ∫_0 ^1 e^t {Σ_(n=1) ^∞ (((−1)^(n−1) )/n) e^(−nat) }dt = Σ_(n=1) ^∞ (((−1)^(n−1) )/n) ∫_0 ^1 e^((1−na)t) dt =Σ_(n=1) ^∞ (((−1)^(n−1) )/n)(1/(1−na)){ e^(1−na) −1} =Σ_(n=1) ^∞ (((−1)^(n−1) e^(1−na) )/(n(1−na))) −Σ_(n=1) ^∞ (((−1)^(n−1) )/(n(1−na))) let w(a) =Σ_(n=1) ^∞ (((−1)^(n−1) )/(n(1−na))) ((w(a))/a) =Σ_(n=1) ^∞ (((−1)^n )/(na(na−1))) =Σ_(n=1) ^∞ (−1)^n ( (1/(na−1)) −(1/(na))) =Σ_(n=1) ^∞ (((−1))/(na−1)) −(1/a) Σ_(n=1) ^∞ (((−1)^n )/n) Σ_(n=1) ^∞ (((−1)^n )/(na−1)) +((ln(2))/a) =....be continued...
$${for}\:\mid{x}\mid<\mathrm{1}\:{ln}^{'} \left(\mathrm{1}+{x}\right)\:=\frac{\mathrm{1}}{\mathrm{1}+{x}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \left(−\mathrm{1}\right)^{{n}} {x}^{{n}} \\ $$$${and}\:{ln}\left(\mathrm{1}+{x}\right)=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}{x}^{{n}+\mathrm{1}} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}{x}^{{n}} \:\Rightarrow \\ $$$${f}\left({a}\right)=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{{t}} \:\left\{\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:\:{e}^{−{nat}} \right\}{dt} \\ $$$$=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:{e}^{\left(\mathrm{1}−{na}\right){t}} {dt} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\frac{\mathrm{1}}{\mathrm{1}−{na}}\left\{\:{e}^{\mathrm{1}−{na}} \:−\mathrm{1}\right\} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:{e}^{\mathrm{1}−{na}} }{{n}\left(\mathrm{1}−{na}\right)} \\ $$$$−\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}\left(\mathrm{1}−{na}\right)} \\ $$$${let}\:{w}\left({a}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}\left(\mathrm{1}−{na}\right)} \\ $$$$\frac{{w}\left({a}\right)}{{a}}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{na}\left({na}−\mathrm{1}\right)} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\left(−\mathrm{1}\right)^{{n}} \left(\:\frac{\mathrm{1}}{{na}−\mathrm{1}}\:−\frac{\mathrm{1}}{{na}}\right) \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)}{{na}−\mathrm{1}}\:−\frac{\mathrm{1}}{{a}}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}} \\ $$$$\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{na}−\mathrm{1}}\:\:+\frac{{ln}\left(\mathrm{2}\right)}{{a}}\:=….{be}\:{continued}… \\ $$
Commented by abdo.msup.com last updated on 05/Jun/18
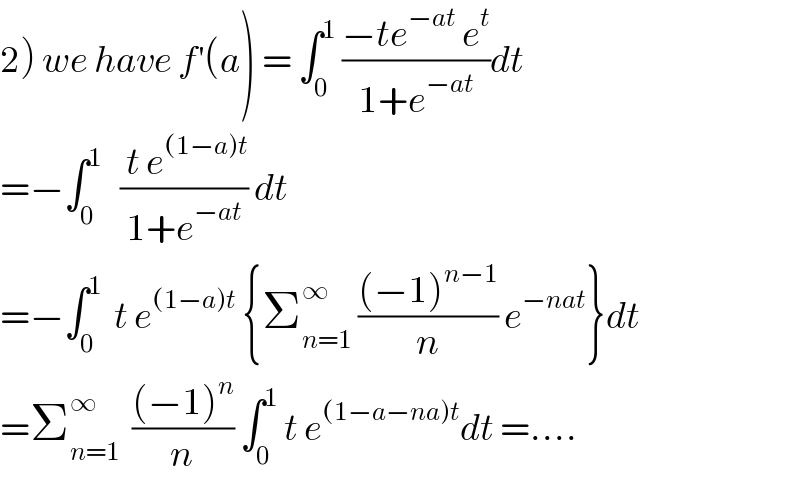
2) we have f^′ (a) = ∫_0 ^1 ((−te^(−at) e^t )/(1+e^(−at) ))dt =−∫_0 ^1 (( t e^((1−a)t) )/(1+e^(−at) )) dt =−∫_0 ^1 t e^((1−a)t) {Σ_(n=1) ^∞ (((−1)^(n−1) )/n) e^(−nat) }dt =Σ_(n=1) ^∞ (((−1)^n )/n) ∫_0 ^1 t e^((1−a−na)t) dt =....
$$\left.\mathrm{2}\right)\:{we}\:{have}\:{f}^{'} \left({a}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{−{te}^{−{at}} \:{e}^{{t}} }{\mathrm{1}+{e}^{−{at}} }{dt} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{\:{t}\:{e}^{\left(\mathrm{1}−{a}\right){t}} }{\mathrm{1}+{e}^{−{at}} }\:{dt}\: \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{t}\:{e}^{\left(\mathrm{1}−{a}\right){t}} \:\left\{\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:{e}^{−{nat}} \right\}{dt} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}\:{e}^{\left(\mathrm{1}−{a}−{na}\right){t}} {dt}\:=…. \\ $$
Commented by abdo.msup.com last updated on 05/Jun/18
3) ∫_0 ^1 e^t ln(1+e^(−3t) )dt = ∫_0 ^1 e^t { Σ_(n=1) ^∞ (((−1)^(n−1) )/n) e^(−3nt) )}dt =Σ_(n=1) ^∞ (((−1)^(n−1) )/n) ∫_0 ^1 e^((1−3n)t) dt =Σ_(n=1) ^∞ (((−1)^(n−1) )/n) (1/(1−3n))[ e^((1−3n)t) ]_0 ^1 =Σ_(n=1) ^∞ (((−1)^(n−1) e^(1−3n) )/(n(1−3n))) −Σ_(n=1) ^∞ (((−1)^(n−1) )/(n(1−3n))) let A_n = Σ_(n=1) ^∞ (((−1)^(n−1) )/(n(1−3n))) (A_n /3) = Σ_(n=1) ^∞ (((−1)^n )/(3n(3n−1))) =Σ_(n=1) ^∞ (−1)^n {(1/(3n−1)) −(1/(3n))} =Σ_(n=1) ^(∞ ) (((−1)^n )/(3n−1)) −(1/3) Σ_(n=1) ^∞ (((−1)^n )/n) =((ln(2))/3) +Σ_(n=1) ^∞ (((−1)^n )/(3n−1)) let f(x)=Σ_(n=1) ^∞ (−1)^n (x^(3n−1) /(3n−1)) f^′ (x) = Σ_(n=1) ^∞ (−1)^n x^(3n−2) = (1/x^2 ) Σ_(n=1) ^∞ (−x^3 )^n = (1/x^2 ) (1/(1+x^3 )) ⇒ f(x)= ∫ (dx/(x^2 (1+x^3 ))) +c ....be continued...
$$\left.\mathrm{3}\right)\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{{t}} \:{ln}\left(\mathrm{1}+{e}^{−\mathrm{3}{t}} \right){dt} \\ $$$$\left.=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{e}^{{t}} \:\left\{\:\sum_{{n}=\mathrm{1}} ^{\infty} \frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:\:{e}^{−\mathrm{3}{nt}} \right)\right\}{dt} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{e}^{\left(\mathrm{1}−\mathrm{3}{n}\right){t}} {dt} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:\frac{\mathrm{1}}{\mathrm{1}−\mathrm{3}{n}}\left[\:{e}^{\left(\mathrm{1}−\mathrm{3}{n}\right){t}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:{e}^{\mathrm{1}−\mathrm{3}{n}} }{{n}\left(\mathrm{1}−\mathrm{3}{n}\right)} \\ $$$$−\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}\left(\mathrm{1}−\mathrm{3}{n}\right)}\:{let} \\ $$$${A}_{{n}} =\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}\left(\mathrm{1}−\mathrm{3}{n}\right)} \\ $$$$\frac{{A}_{{n}} }{\mathrm{3}}\:=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{3}{n}\left(\mathrm{3}{n}−\mathrm{1}\right)} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \left\{\frac{\mathrm{1}}{\mathrm{3}{n}−\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{3}{n}}\right\} \\ $$$$=\sum_{{n}=\mathrm{1}} ^{\infty\:} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{3}{n}−\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{3}}\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}} \\ $$$$=\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{3}}\:+\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{3}{n}−\mathrm{1}} \\ $$$${let}\:{f}\left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:\:\left(−\mathrm{1}\right)^{{n}} \:\frac{{x}^{\mathrm{3}{n}−\mathrm{1}} }{\mathrm{3}{n}−\mathrm{1}} \\ $$$${f}^{'} \left({x}\right)\:=\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:{x}^{\mathrm{3}{n}−\mathrm{2}} \\ $$$$=\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:\sum_{{n}=\mathrm{1}} ^{\infty} \:\left(−{x}^{\mathrm{3}} \right)^{{n}} =\:\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{3}} }\:\Rightarrow \\ $$$${f}\left({x}\right)=\:\int\:\:\:\:\:\frac{{dx}}{{x}^{\mathrm{2}} \left(\mathrm{1}+{x}^{\mathrm{3}} \right)}\:+{c}\:….{be}\:{continued}… \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 05/Jun/18
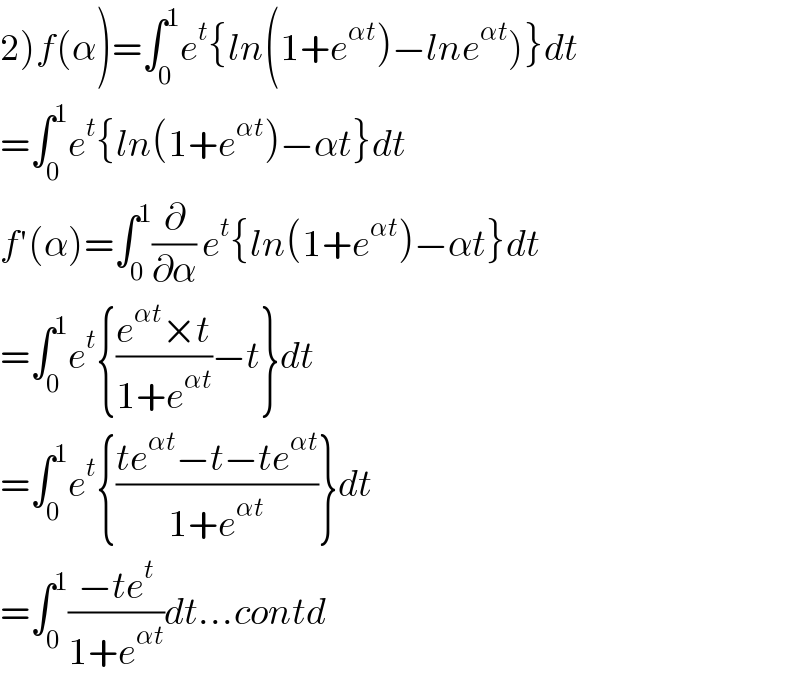
2)f(α)=∫_0 ^1 e^t {ln(1+e^(αt) )−lne^(αt) )}dt =∫_0 ^1 e^t {ln(1+e^(αt) )−αt}dt f′(α)=∫_0 ^1 (∂/∂α) e^t {ln(1+e^(αt) )−αt}dt =∫_0 ^1 e^t {((e^(αt) ×t)/(1+e^(αt) ))−t}dt =∫_0 ^1 e^t {((te^(αt) −t−te^(αt) )/(1+e^(αt) ))}dt =∫_0 ^1 ((−te^t )/(1+e^(αt) ))dt...contd
$$\left.\mathrm{2}\left.\right){f}\left(\alpha\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{t}} \left\{{ln}\left(\mathrm{1}+{e}^{\alpha{t}} \right)−{lne}^{\alpha{t}} \right)\right\}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{t}} \left\{{ln}\left(\mathrm{1}+{e}^{\alpha{t}} \right)−\alpha{t}\right\}{dt} \\ $$$${f}'\left(\alpha\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\partial}{\partial\alpha}\:{e}^{{t}} \left\{{ln}\left(\mathrm{1}+{e}^{\alpha{t}} \right)−\alpha{t}\right\}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{t}} \left\{\frac{{e}^{\alpha{t}} ×{t}}{\mathrm{1}+{e}^{\alpha{t}} }−{t}\right\}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{t}} \left\{\frac{{te}^{\alpha{t}} −{t}−{te}^{\alpha{t}} }{\mathrm{1}+{e}^{\alpha{t}} }\right\}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{−{te}^{{t}} }{\mathrm{1}+{e}^{\alpha{t}} }{dt}…{contd} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *