Question Number 50413 by Abdo msup. last updated on 16/Dec/18
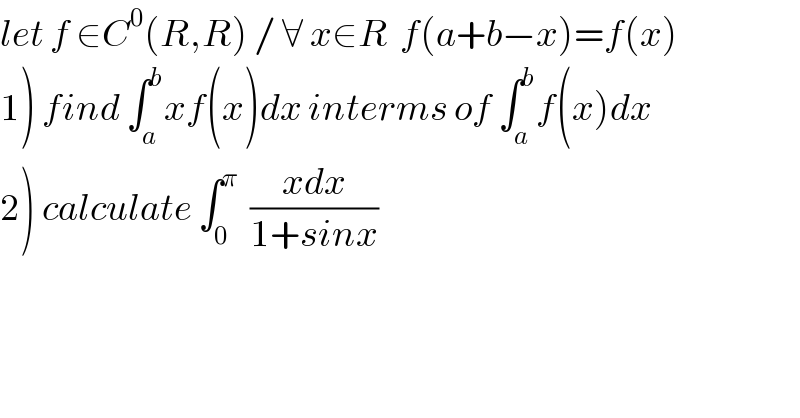
$${let}\:{f}\:\in{C}^{\mathrm{0}} \left({R},{R}\right)\:/\:\forall\:{x}\in{R}\:\:{f}\left({a}+{b}−{x}\right)={f}\left({x}\right) \\ $$$$\left.\mathrm{1}\right)\:{find}\:\int_{{a}} ^{{b}} {xf}\left({x}\right){dx}\:{interms}\:{of}\:\int_{{a}} ^{{b}} {f}\left({x}\right){dx} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{{xdx}}{\mathrm{1}+{sinx}} \\ $$
Commented by Abdo msup. last updated on 24/Dec/18
![1)∫_a ^b xf(x)dx =∫_a ^b xf(a+b−x)dx =_(a+b−x=t ) −∫_b ^a (a+b−t)f(t)dt =∫_a ^b (a+b)f(t) −∫_a ^b tf(t)dt ⇒ 2 ∫_a ^b xf(x)dx =(a+b)∫_a ^b f(t)dt ⇒ ∫_a ^b xf(x)dx =((a+b)/2) ∫_a ^b f(x)dx 2) we have ∫_0 ^π ((xdx)/(1+sinx)) =∫_0 ^π xf(x)dx with f(x)=(1/(1+sinx)) we have f(0+π−x)=(1/(1+sin(π−x))) =f(x) ⇒∫_0 ^π xf(x)dx =(π/2) ∫_0 ^π (dx/(1+sinx)) =_(tan((x/2))=t) (π/2) ∫_0 ^∞ (1/(1+((2t)/(1+t^2 )))) ((2dt)/(1+t^2 )) =π ∫_0 ^∞ (dt/(1+t^2 +2t)) =π ∫_0 ^∞ (dt/((t+1)^2 )) =π [−(1/(t+1))]_0 ^(+∞) = π .](https://www.tinkutara.com/question/Q51145.png)
$$\left.\mathrm{1}\right)\int_{{a}} ^{{b}} {xf}\left({x}\right){dx}\:=\int_{{a}} ^{{b}} {xf}\left({a}+{b}−{x}\right){dx}\: \\ $$$$=_{{a}+{b}−{x}={t}\:} \:\:\:\:−\int_{{b}} ^{{a}} \:\left({a}+{b}−{t}\right){f}\left({t}\right){dt} \\ $$$$=\int_{{a}} ^{{b}} \left({a}+{b}\right){f}\left({t}\right)\:−\int_{{a}} ^{{b}} {tf}\left({t}\right){dt}\:\Rightarrow \\ $$$$\mathrm{2}\:\int_{{a}} ^{{b}} \:{xf}\left({x}\right){dx}\:=\left({a}+{b}\right)\int_{{a}} ^{{b}} \:{f}\left({t}\right){dt}\:\Rightarrow \\ $$$$\int_{{a}} ^{{b}} \:{xf}\left({x}\right){dx}\:=\frac{{a}+{b}}{\mathrm{2}}\:\int_{{a}} ^{{b}} \:{f}\left({x}\right){dx} \\ $$$$\left.\mathrm{2}\right)\:{we}\:{have}\:\int_{\mathrm{0}} ^{\pi} \:\frac{{xdx}}{\mathrm{1}+{sinx}}\:=\int_{\mathrm{0}} ^{\pi} \:{xf}\left({x}\right){dx}\:{with} \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}+{sinx}}\:\:{we}\:{have}\:{f}\left(\mathrm{0}+\pi−{x}\right)=\frac{\mathrm{1}}{\mathrm{1}+{sin}\left(\pi−{x}\right)} \\ $$$$={f}\left({x}\right)\:\Rightarrow\int_{\mathrm{0}} ^{\pi} \:{xf}\left({x}\right){dx}\:=\frac{\pi}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{{dx}}{\mathrm{1}+{sinx}} \\ $$$$=_{{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}} \:\:\frac{\pi}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{\mathrm{1}+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\pi\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} \:+\mathrm{2}{t}}\:=\pi\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{dt}}{\left({t}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\pi\:\left[−\frac{\mathrm{1}}{{t}+\mathrm{1}}\right]_{\mathrm{0}} ^{+\infty} \:=\:\pi\:\:. \\ $$
