Menu Close

let-f-x-0-x-t-1-sint-dt-1-find-a-explicit-form-of-f-x-2-calculate-0-t-1-sint-dt-

Tinku Tara 0 Comments
Pin




Question Number 43337 by math khazana by abdo last updated on 09/Sep/18
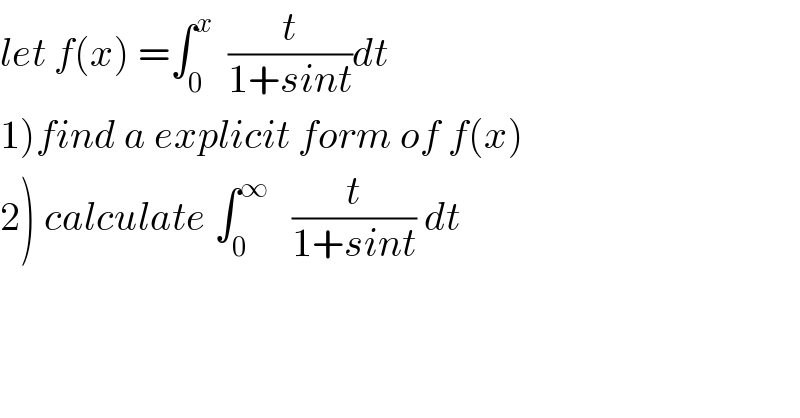
let f(x) =∫_0 ^x (t/(1+sint))dt 1)find a explicit form of f(x) 2) calculate ∫_0 ^∞ (t/(1+sint)) dt
$${let}\:{f}\left({x}\right)\:=\int_{\mathrm{0}} ^{{x}} \:\:\frac{{t}}{\mathrm{1}+{sint}}{dt} \\ $$$$\left.\mathrm{1}\right){find}\:{a}\:{explicit}\:{form}\:{of}\:{f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{t}}{\mathrm{1}+{sint}}\:{dt}\: \\ $$
Commented by maxmathsup by imad last updated on 11/Sep/18
1) changement tan((t/2))=u give f(x)= ∫_0 ^(tan((x/2))) ((2 arctanu)/(1+ ((2u)/(1+u^2 )))) ((2du)/(1+u^2 )) = ∫_0 ^(tan((x/2))) ((4 arctanu)/(1+u^2 +2u))du =4∫_0 ^(tan((x/2))) (( arctanu)/((u+1)^2 )) du by parts we get f(x) =4{ [−(1/(1+u)) arctanu]_0 ^(tan((x/2))) +∫_0 ^(tan((x/2))) (du/((u+1)(1+u^2 ))} =−4 (x/(2(1+tan((x/2))))) +4 ∫_0 ^(tan((x/2))) (du/((u+1)(u^2 +1))) but ∫_0 ^(tan((x/2))) (du/((u+1)(u^2 +1))) =(1/2) ∫_0 ^(tan((x/2))) { (1/(u+1)) −((u−1)/(u^2 +1))}du =(1/2)[ln∣u+1∣]_0 ^(tan((x/2))) −(1/4) [ln(u^2 +1)]_0 ^(tan((x/2))) +(1/2) [ arctanu]_0 ^(tan((x/2))) =(1/2)ln∣1+tan((x/2))∣ −(1/4)ln∣1+tan^2 ((x/2))∣ +(x/4) ⇒ f(x) =((−2x)/(1+tan((x/2)))) +(1/2)ln∣1+tan((x/2))∣ −(1/4)ln∣1+tan^2 ((x/2))∣ +(x/4) .
$$\left.\mathrm{1}\right)\:{changement}\:\:{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u}\:{give}\:{f}\left({x}\right)=\:\int_{\mathrm{0}} ^{{tan}\left(\frac{{x}}{\mathrm{2}}\right)} \:\:\:\frac{\mathrm{2}\:{arctanu}}{\mathrm{1}+\:\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\:\int_{\mathrm{0}} ^{{tan}\left(\frac{{x}}{\mathrm{2}}\right)} \:\:\:\frac{\mathrm{4}\:{arctanu}}{\mathrm{1}+{u}^{\mathrm{2}} \:+\mathrm{2}{u}}{du}\:=\mathrm{4}\int_{\mathrm{0}} ^{{tan}\left(\frac{{x}}{\mathrm{2}}\right)} \:\:\frac{\:{arctanu}}{\left({u}+\mathrm{1}\right)^{\mathrm{2}} }\:{du}\:\:\:\:{by}\:{parts}\:{we}\:{get} \\ $$$${f}\left({x}\right)\:=\mathrm{4}\left\{\:\left[−\frac{\mathrm{1}}{\mathrm{1}+{u}}\:{arctanu}\right]_{\mathrm{0}} ^{{tan}\left(\frac{{x}}{\mathrm{2}}\right)} \:\:+\int_{\mathrm{0}} ^{{tan}\left(\frac{{x}}{\mathrm{2}}\right)} \:\:\:\frac{{du}}{\left({u}+\mathrm{1}\right)\left(\mathrm{1}+{u}^{\mathrm{2}} \right.}\right\} \\ $$$$=−\mathrm{4}\:\:\:\:\:\frac{{x}}{\mathrm{2}\left(\mathrm{1}+{tan}\left(\frac{{x}}{\mathrm{2}}\right)\right)}\:\:+\mathrm{4}\:\:\int_{\mathrm{0}} ^{{tan}\left(\frac{{x}}{\mathrm{2}}\right)} \:\:\:\frac{{du}}{\left({u}+\mathrm{1}\right)\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)}\:{but} \\ $$$$\int_{\mathrm{0}} ^{{tan}\left(\frac{{x}}{\mathrm{2}}\right)} \:\:\:\:\frac{{du}}{\left({u}+\mathrm{1}\right)\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{{tan}\left(\frac{{x}}{\mathrm{2}}\right)} \left\{\:\frac{\mathrm{1}}{{u}+\mathrm{1}}\:−\frac{{u}−\mathrm{1}}{{u}^{\mathrm{2}} +\mathrm{1}}\right\}{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[{ln}\mid{u}+\mathrm{1}\mid\right]_{\mathrm{0}} ^{{tan}\left(\frac{{x}}{\mathrm{2}}\right)} \:\:−\frac{\mathrm{1}}{\mathrm{4}}\:\left[{ln}\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\right]_{\mathrm{0}} ^{{tan}\left(\frac{{x}}{\mathrm{2}}\right)} \:\:+\frac{\mathrm{1}}{\mathrm{2}}\:\left[\:{arctanu}\right]_{\mathrm{0}} ^{{tan}\left(\frac{{x}}{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\mathrm{1}+{tan}\left(\frac{{x}}{\mathrm{2}}\right)\mid\:−\frac{\mathrm{1}}{\mathrm{4}}{ln}\mid\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\mid\:+\frac{{x}}{\mathrm{4}}\:\Rightarrow \\ $$$${f}\left({x}\right)\:=\frac{−\mathrm{2}{x}}{\mathrm{1}+{tan}\left(\frac{{x}}{\mathrm{2}}\right)}\:\:+\frac{\mathrm{1}}{\mathrm{2}}{ln}\mid\mathrm{1}+{tan}\left(\frac{{x}}{\mathrm{2}}\right)\mid\:−\frac{\mathrm{1}}{\mathrm{4}}{ln}\mid\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\mid\:+\frac{{x}}{\mathrm{4}}\:. \\ $$
Commented by maxmathsup by imad last updated on 11/Sep/18
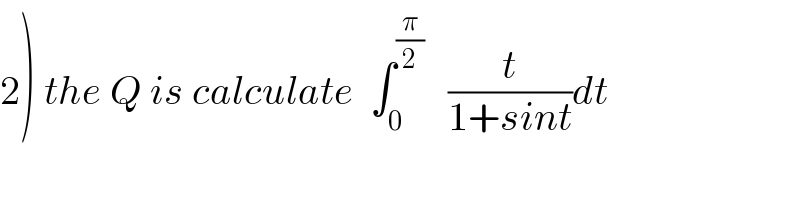
2) the Q is calculate ∫_0 ^(π/2) (t/(1+sint))dt
$$\left.\mathrm{2}\right)\:{the}\:{Q}\:{is}\:{calculate}\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\frac{{t}}{\mathrm{1}+{sint}}{dt} \\ $$
Commented by maxmathsup by imad last updated on 11/Sep/18
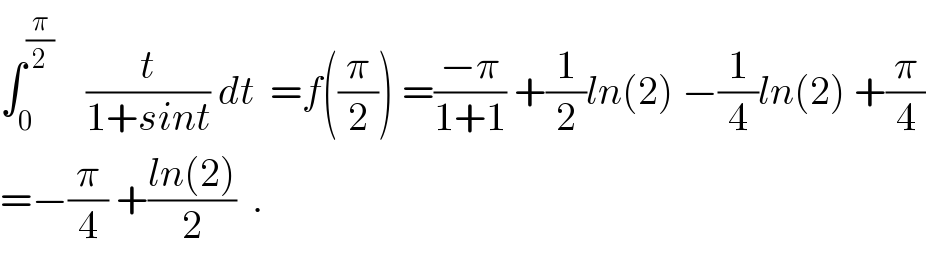
∫_0 ^(π/2) (t/(1+sint)) dt =f((π/2)) =((−π)/(1+1)) +(1/2)ln(2) −(1/4)ln(2) +(π/4) =−(π/4) +((ln(2))/2) .
$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\:\:\frac{{t}}{\mathrm{1}+{sint}}\:{dt}\:\:={f}\left(\frac{\pi}{\mathrm{2}}\right)\:=\frac{−\pi}{\mathrm{1}+\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\:−\frac{\mathrm{1}}{\mathrm{4}}{ln}\left(\mathrm{2}\right)\:+\frac{\pi}{\mathrm{4}} \\ $$$$=−\frac{\pi}{\mathrm{4}}\:+\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}\:\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *