Menu Close

let-f-x-arctan-x-n-with-n-integr-natural-1-calculate-f-x-and-f-2-x-2-calculate-f-n-x-and-f-n-0-3-developp-f-at-integr-serie-

Tinku Tara 0 Comments
Pin




Question Number 96593 by mathmax by abdo last updated on 03/Jun/20
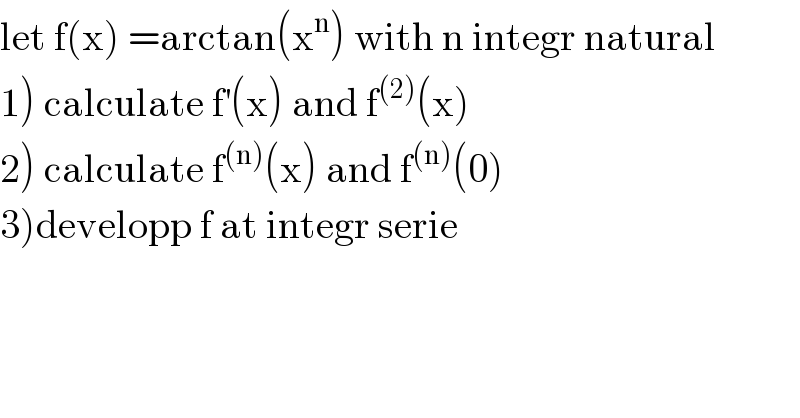
let f(x) =arctan(x^n ) with n integr natural 1) calculate f^′ (x) and f^((2)) (x) 2) calculate f^((n)) (x) and f^((n)) (0) 3)developp f at integr serie
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{arctan}\left(\mathrm{x}^{\mathrm{n}} \right)\:\mathrm{with}\:\mathrm{n}\:\mathrm{integr}\:\mathrm{natural} \\ $$$$\left.\mathrm{1}\right)\:\mathrm{calculate}\:\mathrm{f}^{'} \left(\mathrm{x}\right)\:\mathrm{and}\:\mathrm{f}^{\left(\mathrm{2}\right)} \left(\mathrm{x}\right) \\ $$$$\left.\mathrm{2}\right)\:\mathrm{calculate}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)\:\mathrm{and}\:\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right) \\ $$$$\left.\mathrm{3}\right)\mathrm{developp}\:\mathrm{f}\:\mathrm{at}\:\mathrm{integr}\:\mathrm{serie} \\ $$
Answered by mathmax by abdo last updated on 03/Jun/20
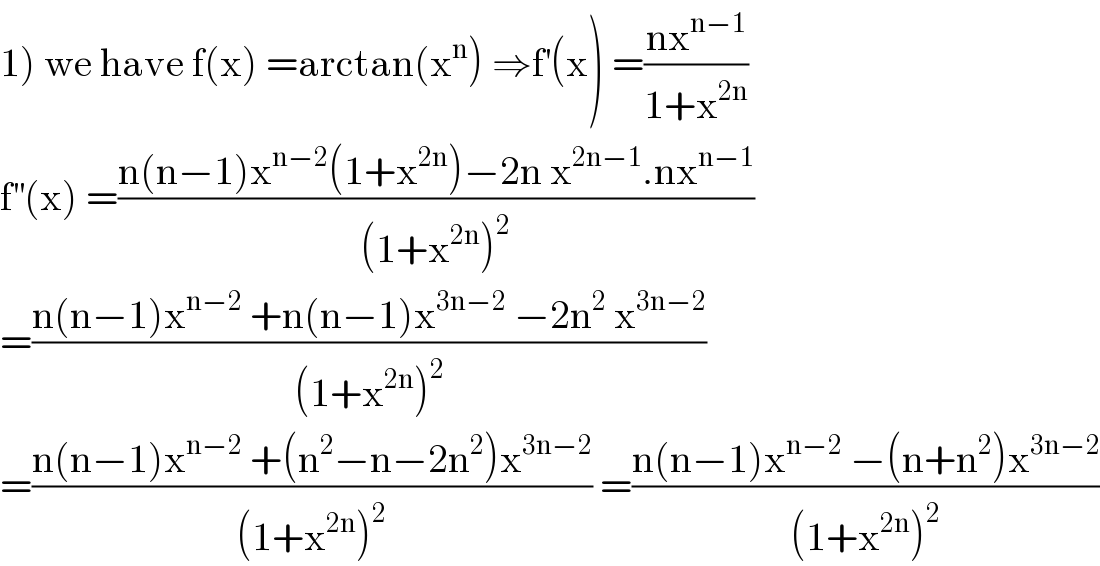
1) we have f(x) =arctan(x^n ) ⇒f^′ (x) =((nx^(n−1) )/(1+x^(2n) )) f^(′′) (x) =((n(n−1)x^(n−2) (1+x^(2n) )−2n x^(2n−1) .nx^(n−1) )/((1+x^(2n) )^2 )) =((n(n−1)x^(n−2) +n(n−1)x^(3n−2) −2n^2 x^(3n−2) )/((1+x^(2n) )^2 )) =((n(n−1)x^(n−2) +(n^2 −n−2n^2 )x^(3n−2) )/((1+x^(2n) )^2 )) =((n(n−1)x^(n−2) −(n+n^2 )x^(3n−2) )/((1+x^(2n) )^2 ))
$$\left.\mathrm{1}\right)\:\mathrm{we}\:\mathrm{have}\:\mathrm{f}\left(\mathrm{x}\right)\:=\mathrm{arctan}\left(\mathrm{x}^{\mathrm{n}} \right)\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{x}\right)\:=\frac{\mathrm{nx}^{\mathrm{n}−\mathrm{1}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2n}} } \\ $$$$\mathrm{f}^{''} \left(\mathrm{x}\right)\:=\frac{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{x}^{\mathrm{n}−\mathrm{2}} \left(\mathrm{1}+\mathrm{x}^{\mathrm{2n}} \right)−\mathrm{2n}\:\mathrm{x}^{\mathrm{2n}−\mathrm{1}} .\mathrm{nx}^{\mathrm{n}−\mathrm{1}} }{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2n}} \right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{x}^{\mathrm{n}−\mathrm{2}} \:+\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{x}^{\mathrm{3n}−\mathrm{2}} \:−\mathrm{2n}^{\mathrm{2}} \:\mathrm{x}^{\mathrm{3n}−\mathrm{2}} }{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2n}} \right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{x}^{\mathrm{n}−\mathrm{2}} \:+\left(\mathrm{n}^{\mathrm{2}} −\mathrm{n}−\mathrm{2n}^{\mathrm{2}} \right)\mathrm{x}^{\mathrm{3n}−\mathrm{2}} }{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2n}} \right)^{\mathrm{2}} }\:=\frac{\mathrm{n}\left(\mathrm{n}−\mathrm{1}\right)\mathrm{x}^{\mathrm{n}−\mathrm{2}} \:−\left(\mathrm{n}+\mathrm{n}^{\mathrm{2}} \right)\mathrm{x}^{\mathrm{3n}−\mathrm{2}} }{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2n}} \right)^{\mathrm{2}} } \\ $$
Answered by mathmax by abdo last updated on 03/Jun/20
2)we have f^′ (x) =((nx^(n−1) )/(1+x^(2n) )) poles of f^(′?) x^(2n) +1 =0 ⇒x^(2n) =e^(i(2k+1)π) ⇒x_k =e^(i(((2k+1)π)/(2n))) k∈[[0,2n−1]] ⇒f^′ (x) =((nx^(n−1) )/(Π_(k=0) ^(2n−1) (x−x_k ))) =Σ_(k=0) ^(2n−1) (a_k /(x−x_k )) , a_k =((nx_k ^(n−1) )/(2n x_k ^(2n−1) )) =(1/2)×(x_k ^n /((−1))) =−(1/2) e^(i(((2k+1)π)/2)) ⇒f^′ (x) =−(1/2) Σ_(k=0) ^(2n−1) (e^(i(((2k+1)π)/2))) /(x−x_k )) ⇒ f^((p)) (x) =−(1/2) Σ_(k=0) ^(2n−1) e^(i(πk +(π/2))) {(1/(x−x_k ))}^((p−1)) =−(1/2)Σ_(k=0) ^(2n−1) i(−1)^k ×(((−1)^(p−1) (p−1)!)/((x−x_k )^p )) =((i(−1)^p (p−1)!)/2) Σ_(k=0) ^(2n−1) (((−1)^k )/((x−x_k )^p )) p=n ⇒f^((n)) (x) =(i/2)(−1)^n (n−1)!Σ_(k=0) ^(2n−1) (((−1)^k )/((x−x_k )^n )) f^((n)) (0) =(i/2)(−1)^n (n−1)! Σ_(k=0) ^(2n−1) (((−1)^k )/((−1)^n x_k ^n )) =(i/2)(n−1)! Σ_(k=0) ^(2n−1) (((−1)^k )/(i(−1)^k )) =(1/2) Σ_(k=0) ^(2n−1) (1) =n ⇒f^((n)) (0) =n
$$\left.\mathrm{2}\right)\mathrm{we}\:\mathrm{have}\:\mathrm{f}^{'} \left(\mathrm{x}\right)\:=\frac{\mathrm{nx}^{\mathrm{n}−\mathrm{1}} }{\mathrm{1}+\mathrm{x}^{\mathrm{2n}} }\:\mathrm{poles}\:\mathrm{of}\:\mathrm{f}^{'?} \\ $$$$\mathrm{x}^{\mathrm{2n}} \:+\mathrm{1}\:=\mathrm{0}\:\Rightarrow\mathrm{x}^{\mathrm{2n}} \:=\mathrm{e}^{\mathrm{i}\left(\mathrm{2k}+\mathrm{1}\right)\pi} \:\Rightarrow\mathrm{x}_{\mathrm{k}} =\mathrm{e}^{\mathrm{i}\frac{\left(\mathrm{2k}+\mathrm{1}\right)\pi}{\mathrm{2n}}} \:\:\:\:\mathrm{k}\in\left[\left[\mathrm{0},\mathrm{2n}−\mathrm{1}\right]\right] \\ $$$$\Rightarrow\mathrm{f}^{'} \left(\mathrm{x}\right)\:=\frac{\mathrm{nx}^{\mathrm{n}−\mathrm{1}} }{\prod_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{1}} \left(\mathrm{x}−\mathrm{x}_{\mathrm{k}} \right)}\:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{1}} \:\frac{\mathrm{a}_{\mathrm{k}} }{\mathrm{x}−\mathrm{x}_{\mathrm{k}} }\:\:\:\:,\:\:\mathrm{a}_{\mathrm{k}} =\frac{\mathrm{nx}_{\mathrm{k}} ^{\mathrm{n}−\mathrm{1}} }{\mathrm{2n}\:\mathrm{x}_{\mathrm{k}} ^{\mathrm{2n}−\mathrm{1}} }\:=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{x}_{\mathrm{k}} ^{\mathrm{n}} }{\left(−\mathrm{1}\right)} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{e}^{\mathrm{i}\frac{\left(\mathrm{2k}+\mathrm{1}\right)\pi}{\mathrm{2}}} \:\Rightarrow\mathrm{f}^{'} \left(\mathrm{x}\right)\:=−\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{1}} \:\frac{\mathrm{e}^{\mathrm{i}\left(\frac{\left.\mathrm{2k}+\mathrm{1}\right)\pi}{\mathrm{2}}\right)} }{\mathrm{x}−\mathrm{x}_{\mathrm{k}} }\:\Rightarrow \\ $$$$\mathrm{f}^{\left(\mathrm{p}\right)} \left(\mathrm{x}\right)\:=−\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{1}} \:\mathrm{e}^{\mathrm{i}\left(\pi\mathrm{k}\:+\frac{\pi}{\mathrm{2}}\right)} \:\left\{\frac{\mathrm{1}}{\mathrm{x}−\mathrm{x}_{\mathrm{k}} }\right\}^{\left(\mathrm{p}−\mathrm{1}\right)} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{1}} \:\mathrm{i}\left(−\mathrm{1}\right)^{\mathrm{k}} ×\frac{\left(−\mathrm{1}\right)^{\mathrm{p}−\mathrm{1}} \:\left(\mathrm{p}−\mathrm{1}\right)!}{\left(\mathrm{x}−\mathrm{x}_{\mathrm{k}} \right)^{\mathrm{p}} } \\ $$$$=\frac{\mathrm{i}\left(−\mathrm{1}\right)^{\mathrm{p}} \left(\mathrm{p}−\mathrm{1}\right)!}{\mathrm{2}}\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\left(\mathrm{x}−\mathrm{x}_{\mathrm{k}} \right)^{\mathrm{p}} } \\ $$$$\mathrm{p}=\mathrm{n}\:\Rightarrow\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{x}\right)\:=\frac{\mathrm{i}}{\mathrm{2}}\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\mathrm{n}−\mathrm{1}\right)!\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\left(\mathrm{x}−\mathrm{x}_{\mathrm{k}} \right)^{\mathrm{n}} } \\ $$$$\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right)\:=\frac{\mathrm{i}}{\mathrm{2}}\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\mathrm{n}−\mathrm{1}\right)!\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{x}_{\mathrm{k}} ^{\mathrm{n}} } \\ $$$$=\frac{\mathrm{i}}{\mathrm{2}}\left(\mathrm{n}−\mathrm{1}\right)!\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\mathrm{i}\left(−\mathrm{1}\right)^{\mathrm{k}} }\:=\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{1}} \left(\mathrm{1}\right)\:=\mathrm{n}\:\Rightarrow\mathrm{f}^{\left(\mathrm{n}\right)} \left(\mathrm{0}\right)\:=\mathrm{n} \\ $$
Commented by mathmax by abdo last updated on 03/Jun/20
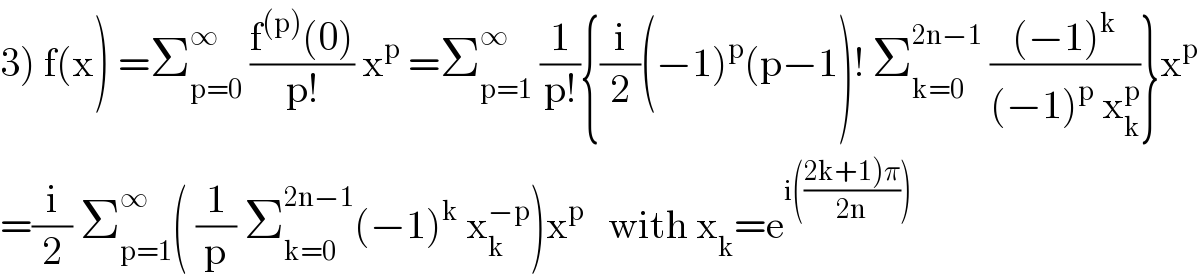
3) f(x) =Σ_(p=0) ^∞ ((f^((p)) (0))/(p!)) x^p =Σ_(p=1) ^∞ (1/(p!)){(i/2)(−1)^p (p−1)! Σ_(k=0) ^(2n−1) (((−1)^k )/((−1)^p x_k ^p ))}x^p =(i/2) Σ_(p=1) ^∞ ( (1/p) Σ_(k=0) ^(2n−1) (−1)^k x_k ^(−p) )x^p with x_k =e^(i(((2k+1)π)/(2n))))
$$\left.\mathrm{3}\right)\:\mathrm{f}\left(\mathrm{x}\right)\:=\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{f}^{\left(\mathrm{p}\right)} \left(\mathrm{0}\right)}{\mathrm{p}!}\:\mathrm{x}^{\mathrm{p}} \:=\sum_{\mathrm{p}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{p}!}\left\{\frac{\mathrm{i}}{\mathrm{2}}\left(−\mathrm{1}\right)^{\mathrm{p}} \left(\mathrm{p}−\mathrm{1}\right)!\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{1}} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} }{\left(−\mathrm{1}\right)^{\mathrm{p}} \:\mathrm{x}_{\mathrm{k}} ^{\mathrm{p}} }\right\}\mathrm{x}^{\mathrm{p}} \\ $$$$=\frac{\mathrm{i}}{\mathrm{2}}\:\sum_{\mathrm{p}=\mathrm{1}} ^{\infty} \left(\:\frac{\mathrm{1}}{\mathrm{p}}\:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}−\mathrm{1}} \left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{x}_{\mathrm{k}} ^{−\mathrm{p}} \right)\mathrm{x}^{\mathrm{p}} \:\:\:\mathrm{with}\:\mathrm{x}_{\mathrm{k}} =\mathrm{e}^{\mathrm{i}\left(\frac{\left.\mathrm{2k}+\mathrm{1}\right)\pi}{\mathrm{2n}}\right)} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *