Question Number 28533 by abdo imad last updated on 26/Jan/18
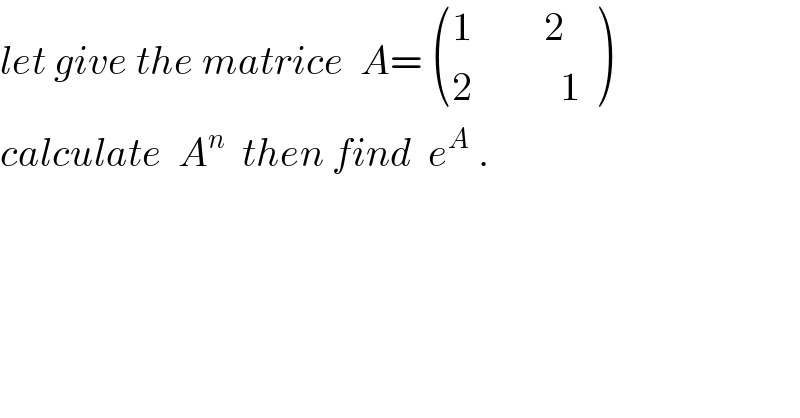
$${let}\:{give}\:{the}\:{matrice}\:\:{A}=\:\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:\:\:\mathrm{2}\:\:\:}\\{\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$${calculate}\:\:{A}^{{n}} \:\:{then}\:{find}\:\:{e}^{{A}} \:. \\ $$
Commented by abdo imad last updated on 28/Jan/18
![we have A = I +2J with I = (((1 0)),((0 1)) ) and J= (((0 1)),((1 0 )) ) we have J^2 = I ⇒ J^(2n) =I and J^(2n+1) =J A= I +2J with the condition IJ=JI A^n =(2J +I)^n = Σ_(k=0) ^n C_n ^k (2J)^k = Σ_(k=0) ^n 2^k C_n ^k J^k = Σ(_(k=2p) ...) +Σ_(k=2p+1) (...) = Σ_(p=0) ^([(n/2)]) 2^(2p) C_n ^(2p ) I +Σ_(p=0) ^([((n−1)/2)]) 2^(2p+1) C_n ^(2p+1) J = (((Σ_(p=0) ^([(n/2)]) 2^(2p) C_n ^(2p) 0 )),((0 Σ_(p=0) ^([(n/2)]) 2^(2p) C_n ^(2p) )) ) + (((0 Σ_(p=0) ^([((n−1)/2)]) 2^(2p+1) C_n ^(2p+1) )),((Σ_(p=0) ^([((n−1)/2)]) 2^(2p+1) C_n ^(2p+1) 0)) ) = (((x_n y_n )),(y_(n x_n ) ) ) with x_n = Σ_(p=0) ^([(n/2)]) 2^(2p) C_n ^(2p) and y_n =Σ_(p=0) ^([((n−1)/2)]) 2^(2p+1) C_n ^(2p+1) . e^A = Σ_(n=0) ^∞ (A^n /(n!))= ((( Σ (x_n /(n!)) Σ(y_n /(n!)) )),((Σ(y_n /(n!)) Σ(x_n /(n!)) )) )](https://www.tinkutara.com/question/Q28669.png)
$${we}\:{have}\:\:{A}\:=\:{I}\:\:+\mathrm{2}{J}\:\:{with}\:\:\:{I}\:=\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$${and}\:\:{J}=\:\begin{pmatrix}{\mathrm{0}\:\:\:\:\:\:\mathrm{1}}\\{\mathrm{1}\:\:\:\:\:\:\:\mathrm{0}\:}\end{pmatrix} \\ $$$${we}\:{have}\:{J}^{\mathrm{2}} =\:{I}\:\Rightarrow\:{J}^{\mathrm{2}{n}} \:={I}\:{and}\:{J}^{\mathrm{2}{n}+\mathrm{1}} ={J} \\ $$$${A}=\:{I}\:+\mathrm{2}{J}\:\:{with}\:{the}\:{condition}\:{IJ}={JI} \\ $$$${A}^{{n}} =\left(\mathrm{2}{J}\:+{I}\right)^{{n}} =\:\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\left(\mathrm{2}{J}\right)^{{k}} \: \\ $$$$=\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\mathrm{2}^{{k}} \:\:{C}_{{n}} ^{{k}} \:{J}^{{k}} \:=\:\Sigma\left(_{{k}=\mathrm{2}{p}} …\right)\:+\sum_{{k}=\mathrm{2}{p}+\mathrm{1}} \:\:\:\left(…\right) \\ $$$$=\:\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}}{\mathrm{2}}\right]} \:\:\:\mathrm{2}^{\mathrm{2}{p}} \:{C}_{{n}} ^{\mathrm{2}{p}\:} {I}\:\:+\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:\:\mathrm{2}^{\mathrm{2}{p}+\mathrm{1}} \:\:{C}_{{n}} ^{\mathrm{2}{p}+\mathrm{1}} \:\:{J} \\ $$$$=\begin{pmatrix}{\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}}{\mathrm{2}}\right]} \:\mathrm{2}^{\mathrm{2}{p}} \:{C}_{{n}} ^{\mathrm{2}{p}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}}{\mathrm{2}}\right]} \:\mathrm{2}^{\mathrm{2}{p}} \:{C}_{{n}} ^{\mathrm{2}{p}} }\end{pmatrix} \\ $$$$+\begin{pmatrix}{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:\mathrm{2}^{\mathrm{2}{p}+\mathrm{1}} \:\:{C}_{{n}} ^{\mathrm{2}{p}+\mathrm{1}} \:\:\:}\\{\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:\mathrm{2}^{\mathrm{2}{p}+\mathrm{1}} \:{C}_{{n}} ^{\mathrm{2}{p}+\mathrm{1}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}}\end{pmatrix} \\ $$$$=\:\begin{pmatrix}{{x}_{{n}} \:\:\:\:\:\:\:\:\:\:{y}_{{n}} }\\{{y}_{{n}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{x}_{{n}} } }\end{pmatrix} \\ $$$${with}\:\:\:{x}_{{n}} =\:\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}}{\mathrm{2}}\right]} \:\:\:\mathrm{2}^{\mathrm{2}{p}} \:\:{C}_{{n}} ^{\mathrm{2}{p}} \:\:{and}\:{y}_{{n}} =\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:\mathrm{2}^{\mathrm{2}{p}+\mathrm{1}} \:{C}_{{n}} ^{\mathrm{2}{p}+\mathrm{1}} \:\:\:. \\ $$$${e}^{{A}} \:\:=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\:\frac{{A}^{{n}} }{{n}!}=\begin{pmatrix}{\:\Sigma\:\frac{{x}_{{n}} }{{n}!}\:\:\:\:\:\:\:\:\:\:\:\:\Sigma\frac{{y}_{{n}} }{{n}!}\:\:\:\:\:}\\{\Sigma\frac{{y}_{{n}} }{{n}!}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Sigma\frac{{x}_{{n}} }{{n}!}\:}\end{pmatrix} \\ $$$$ \\ $$
