Question Number 27663 by abdo imad last updated on 12/Jan/18
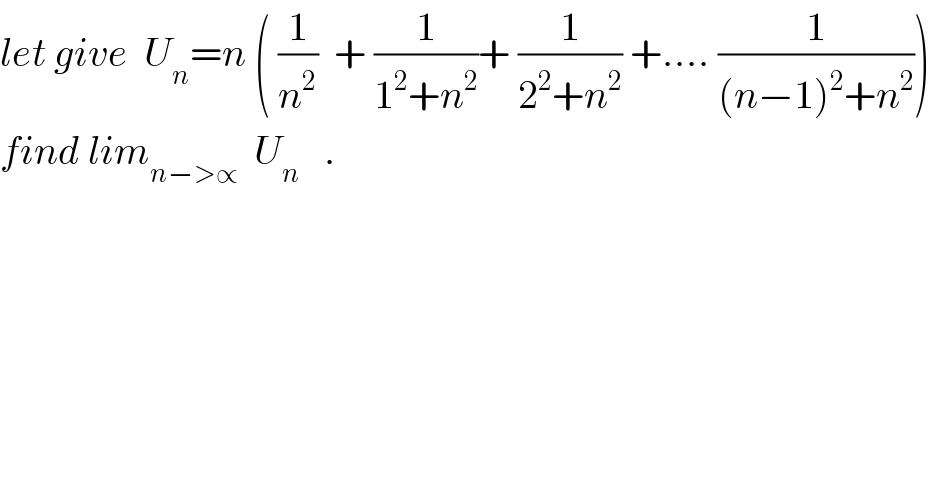
$${let}\:{give}\:\:{U}_{{n}} ={n}\:\left(\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\:\:+\:\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} +{n}^{\mathrm{2}} }+\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} +{n}^{\mathrm{2}} }\:+….\:\frac{\mathrm{1}}{\left({n}−\mathrm{1}\right)^{\mathrm{2}} +{n}^{\mathrm{2}} }\right) \\ $$$${find}\:{lim}_{{n}−>\propto} \:\:{U}_{{n}} \:\:\:. \\ $$$$ \\ $$
Commented by abdo imad last updated on 13/Jan/18
![we have U_n = n Σ_(k=0) ^(n−1) (1/(k^2 +n^2 ))= (1/n) Σ_(k=0) ^(n−1) (1/(1+((k/n))^2 )) U_n is aRieman sum and lim_(n−>∝) U_n = lim_(n−>∝ ) ((1−0)/n) Σ_(k=0) ^(n−1) (1/(1+(((k(1−0))/n))^2 )) = ∫_0 ^1 (dx/(1+x^2 )) ^ =[arctanx]_0 ^1 = (π/4) .](https://www.tinkutara.com/question/Q27739.png)
$${we}\:{have}\:{U}_{{n}} =\:{n}\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\:\frac{\mathrm{1}}{{k}^{\mathrm{2}} \:+{n}^{\mathrm{2}} }=\:\frac{\mathrm{1}}{{n}}\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\frac{\mathrm{1}}{\mathrm{1}+\left(\frac{{k}}{{n}}\right)^{\mathrm{2}} } \\ $$$${U}_{{n}} \:\:{is}\:{aRieman}\:{sum}\:{and} \\ $$$${lim}_{{n}−>\propto} {U}_{{n}} \:=\:{lim}_{{n}−>\propto\:} \:\:\frac{\mathrm{1}−\mathrm{0}}{{n}}\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:\frac{\mathrm{1}}{\mathrm{1}+\left(\frac{{k}\left(\mathrm{1}−\mathrm{0}\right)}{{n}}\right)^{\mathrm{2}} } \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\:^{} =\left[{arctanx}\right]_{\mathrm{0}} ^{\mathrm{1}} =\:\frac{\pi}{\mathrm{4}}\:. \\ $$
