Menu Close

let-p-x-x-2n-x-n-1-1-determine-the-roots-of-p-x-2-factorize-inside-C-x-the-polynom-p-x-3-solve-p-x-0-and-p-x-2-

Tinku Tara 0 Comments
Pin




Question Number 49647 by maxmathsup by imad last updated on 08/Dec/18
let p(x) =x^(2n) −x^n +1 1) determine the roots of p(x) 2) factorize inside C[x] the polynom p(x) . 3)solve p(x)=0 and p(x) =2
$${let}\:{p}\left({x}\right)\:={x}^{\mathrm{2}{n}} \:−{x}^{{n}} \:+\mathrm{1} \\ $$$$\left.\mathrm{1}\right)\:{determine}\:{the}\:{roots}\:{of}\:{p}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{factorize}\:{inside}\:{C}\left[{x}\right]\:{the}\:{polynom}\:{p}\left({x}\right)\:. \\ $$$$\left.\mathrm{3}\right){solve}\:{p}\left({x}\right)=\mathrm{0}\:\:{and}\:{p}\left({x}\right)\:=\mathrm{2} \\ $$
Commented by maxmathsup by imad last updated on 08/Dec/18
let put x^n =t ⇒x^(2n) −x^n +1 =t^2 −t +1 Δ = 1−4 =−3 =(i(√3))^2 ⇒t_1 = ((1+i(√3))/2) and t_2 =((1−i(√3))/2) ⇒t_1 =e^((iπ)/3) and t_2 =e^(−((iπ)/3)) ⇒p(x)=(x^n −e^((iπ)/3) )(x^n −e^(−((iπ)/3)) )so p(x)=0 ⇔x^n =e^((iπ)/3) or x^n =e^(−((iπ)/3)) let solve x^n =e^((iπ)/3) x=r e^(iθ) ⇒r^n e^(inθ) =e^((iπ)/3) ⇒r=1 and nθ=(π/3)+2kπ ⇒ θ_k =(π/(3n)) +((2kπ)/n) with k∈[[0,n−1]] ⇒ x_k =e^(i((π/(3n))+((2kπ)/n))) also x^n =e^(−((iπ)/3)) give t_k =e^(i(−(π/(3n))+((2kπ)/n))) k∈[[0,n−1]] so the roots of p(x) are x_k and t_k . 2)p(x) =Π_(k=0) ^(n−1) (x−x_k ) Π_(k=0) ^(n−1) (x−t_k ) =Π_(k=0) ^(n−1) (x−x_k )(x−x_k ^− ) with x_k = e^(i((π/(3n))+((2kπ)/n)))
$${let}\:{put}\:{x}^{{n}} \:={t}\:\Rightarrow{x}^{\mathrm{2}{n}} −{x}^{{n}} \:+\mathrm{1}\:={t}^{\mathrm{2}} −{t}\:+\mathrm{1}\: \\ $$$$\Delta\:=\:\mathrm{1}−\mathrm{4}\:=−\mathrm{3}\:=\left({i}\sqrt{\mathrm{3}}\right)^{\mathrm{2}} \:\Rightarrow{t}_{\mathrm{1}} =\:\frac{\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:{and}\:{t}_{\mathrm{2}} =\frac{\mathrm{1}−{i}\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$\Rightarrow{t}_{\mathrm{1}} ={e}^{\frac{{i}\pi}{\mathrm{3}}} \:\:{and}\:{t}_{\mathrm{2}} ={e}^{−\frac{{i}\pi}{\mathrm{3}}} \:\Rightarrow{p}\left({x}\right)=\left({x}^{{n}} \:−{e}^{\frac{{i}\pi}{\mathrm{3}}} \right)\left({x}^{{n}} −{e}^{−\frac{{i}\pi}{\mathrm{3}}} \right){so}\:{p}\left({x}\right)=\mathrm{0}\:\Leftrightarrow{x}^{{n}} ={e}^{\frac{{i}\pi}{\mathrm{3}}} \\ $$$${or}\:{x}^{{n}} ={e}^{−\frac{{i}\pi}{\mathrm{3}}} \:\:\:\:\:{let}\:{solve}\:{x}^{{n}} ={e}^{\frac{{i}\pi}{\mathrm{3}}} \:\:\:{x}={r}\:{e}^{{i}\theta} \:\Rightarrow{r}^{{n}} \:{e}^{{in}\theta} ={e}^{\frac{{i}\pi}{\mathrm{3}}} \:\Rightarrow{r}=\mathrm{1}\:{and}\:{n}\theta=\frac{\pi}{\mathrm{3}}+\mathrm{2}{k}\pi\:\Rightarrow \\ $$$$\theta_{{k}} =\frac{\pi}{\mathrm{3}{n}}\:+\frac{\mathrm{2}{k}\pi}{{n}}\:\:{with}\:{k}\in\left[\left[\mathrm{0},{n}−\mathrm{1}\right]\right]\:\:\Rightarrow\:{x}_{{k}} ={e}^{{i}\left(\frac{\pi}{\mathrm{3}{n}}+\frac{\mathrm{2}{k}\pi}{{n}}\right)} \\ $$$${also}\:{x}^{{n}} ={e}^{−\frac{{i}\pi}{\mathrm{3}}} \:\:{give}\:{t}_{{k}} ={e}^{{i}\left(−\frac{\pi}{\mathrm{3}{n}}+\frac{\mathrm{2}{k}\pi}{{n}}\right)} \:\:\:{k}\in\left[\left[\mathrm{0},{n}−\mathrm{1}\right]\right]\:{so}\:{the}\:{roots}\:{of}\:{p}\left({x}\right)\:{are} \\ $$$${x}_{{k}} \:{and}\:{t}_{{k}} . \\ $$$$\left.\mathrm{2}\right){p}\left({x}\right)\:=\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left({x}−{x}_{{k}} \right)\:\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left({x}−{t}_{{k}} \right) \\ $$$$=\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \left({x}−{x}_{{k}} \right)\left({x}−\overset{−} {{x}}_{{k}} \right)\:\:\:\:{with}\:{x}_{{k}} =\:{e}^{{i}\left(\frac{\pi}{\mathrm{3}{n}}+\frac{\mathrm{2}{k}\pi}{{n}}\right)} \\ $$
Commented by maxmathsup by imad last updated on 08/Dec/18
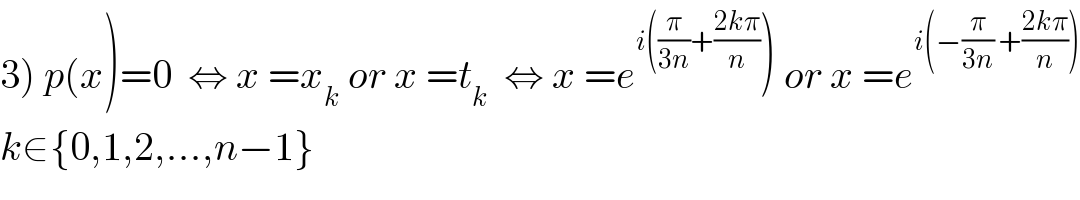
3) p(x)=0 ⇔ x =x_k or x =t_k ⇔ x =e^(i((π/(3n))+((2kπ)/n)) ) or x =e^(i(−(π/(3n)) +((2kπ)/n))) k∈{0,1,2,...,n−1}
$$\left.\mathrm{3}\left.\right)\:{p}\left({x}\right)=\mathrm{0}\:\:\Leftrightarrow\:{x}\:={x}_{{k}} \:{or}\:{x}\:={t}_{{k}} \:\:\Leftrightarrow\:{x}\:={e}^{{i}\left(\frac{\pi}{\mathrm{3}{n}}+\frac{\mathrm{2}{k}\pi}{{n}}\right.} \right)\:{or}\:{x}\:={e}^{{i}\left(−\frac{\pi}{\mathrm{3}{n}}\:+\frac{\mathrm{2}{k}\pi}{{n}}\right)} \\ $$$${k}\in\left\{\mathrm{0},\mathrm{1},\mathrm{2},…,{n}−\mathrm{1}\right\} \\ $$
Commented by maxmathsup by imad last updated on 08/Dec/18
p(x)=2 ⇒x^(2n) −x^n +1=2 ⇒x^(2n) −x^n −1 =0 Δ =1+4 =5 ⇒x^n =((1+(√5))/2) or x^n =((1−(√5))/2) x^n =a (a=((1+(√5))/2)) ⇒ x^n =(^n (√a))^n ⇒ ((x/((^n (√a)))))^n =e^(i(2kπ)) ⇒ (x/((^n (√a)))) = e^((i2kπ)/n) ⇒x_k =^n (√a) e^((i2kπ)/n) with k from[[0,n−1]] also x^n =((1−(√5))/2) (=α) ⇒x =^n (√α)e^((i2kπ)/n) with 0≤k≤n−1
$${p}\left({x}\right)=\mathrm{2}\:\Rightarrow{x}^{\mathrm{2}{n}} −{x}^{{n}} \:+\mathrm{1}=\mathrm{2}\:\Rightarrow{x}^{\mathrm{2}{n}} −{x}^{{n}} −\mathrm{1}\:=\mathrm{0} \\ $$$$\Delta\:=\mathrm{1}+\mathrm{4}\:=\mathrm{5}\:\Rightarrow{x}^{{n}} \:=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:{or}\:{x}^{{n}} \:=\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${x}^{{n}} \:={a}\:\:\:\:\left({a}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)\:\:\Rightarrow\:{x}^{{n}} \:=\left(^{{n}} \sqrt{{a}}\right)^{{n}} \:\Rightarrow\:\left(\frac{{x}}{\left(^{{n}} \sqrt{{a}}\right)}\right)^{{n}} \:={e}^{{i}\left(\mathrm{2}{k}\pi\right)} \:\Rightarrow \\ $$$$\frac{{x}}{\left(^{{n}} \sqrt{{a}}\right)}\:=\:{e}^{\frac{{i}\mathrm{2}{k}\pi}{{n}}} \:\Rightarrow{x}_{{k}} =^{{n}} \sqrt{{a}}\:{e}^{\frac{{i}\mathrm{2}{k}\pi}{{n}}} \:\:\:\:{with}\:{k}\:{from}\left[\left[\mathrm{0},{n}−\mathrm{1}\right]\right] \\ $$$${also}\:{x}^{{n}} =\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\:\:\left(=\alpha\right)\:\:\Rightarrow{x}\:=^{{n}} \sqrt{\alpha}{e}^{\frac{{i}\mathrm{2}{k}\pi}{{n}}} \:\:{with}\:\mathrm{0}\leqslant{k}\leqslant{n}−\mathrm{1} \\ $$
Answered by Smail last updated on 08/Dec/18
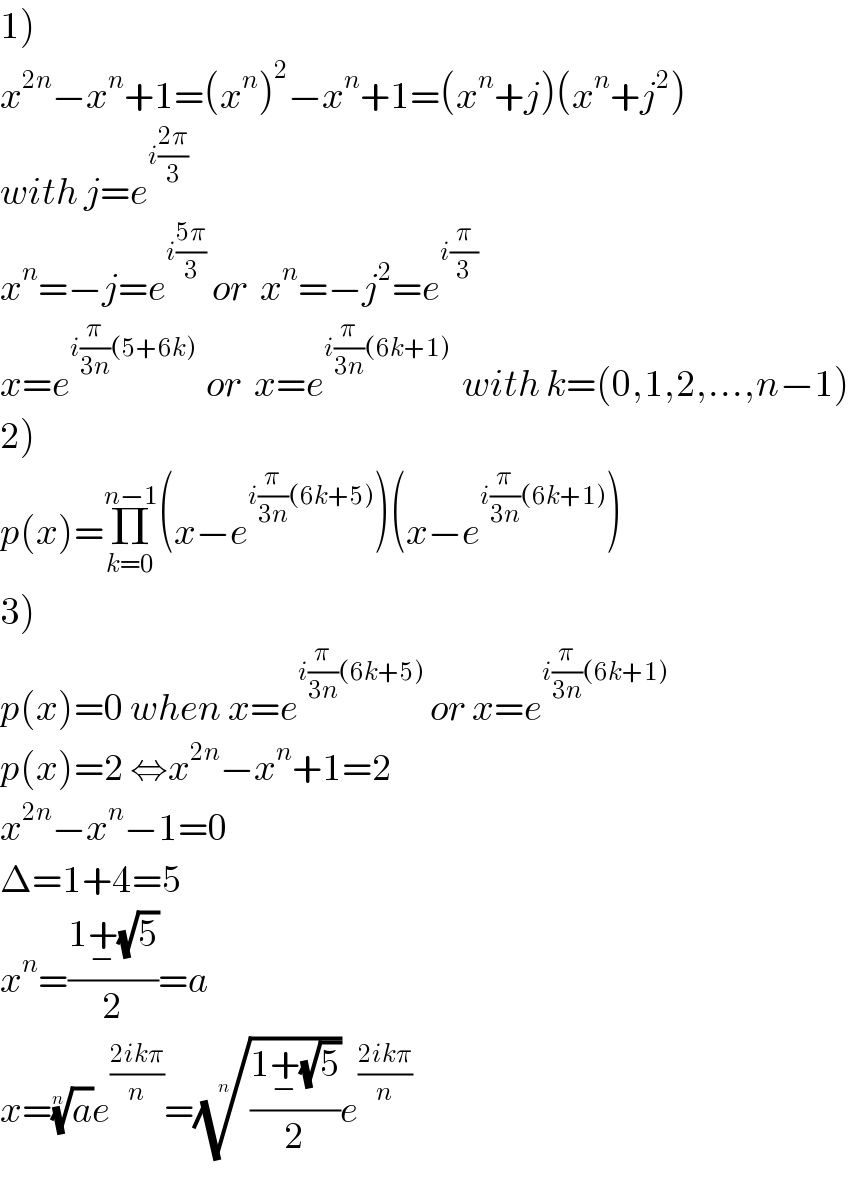
1) x^(2n) −x^n +1=(x^n )^2 −x^n +1=(x^n +j)(x^n +j^2 ) with j=e^(i((2π)/3)) x^n =−j=e^(i((5π)/3)) or x^n =−j^2 =e^(i(π/3)) x=e^(i(π/(3n))(5+6k) ) or x=e^(i(π/(3n))(6k+1)) with k=(0,1,2,...,n−1) 2) p(x)=Π_(k=0) ^(n−1) (x−e^(i(π/(3n))(6k+5)) )(x−e^(i(π/(3n))(6k+1)) ) 3) p(x)=0 when x=e^(i(π/(3n))(6k+5)) or x=e^(i(π/(3n))(6k+1)) p(x)=2 ⇔x^(2n) −x^n +1=2 x^(2n) −x^n −1=0 Δ=1+4=5 x^n =((1+_− (√5))/2)=a x=(a)^(1/n) e^((2ikπ)/n) =(((1+_− (√5))/2))^(1/n) e^((2ikπ)/n)
$$\left.\mathrm{1}\right) \\ $$$${x}^{\mathrm{2}{n}} −{x}^{{n}} +\mathrm{1}=\left({x}^{{n}} \right)^{\mathrm{2}} −{x}^{{n}} +\mathrm{1}=\left({x}^{{n}} +{j}\right)\left({x}^{{n}} +{j}^{\mathrm{2}} \right) \\ $$$${with}\:{j}={e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \\ $$$${x}^{{n}} =−{j}={e}^{{i}\frac{\mathrm{5}\pi}{\mathrm{3}}} \:{or}\:\:{x}^{{n}} =−{j}^{\mathrm{2}} ={e}^{{i}\frac{\pi}{\mathrm{3}}} \\ $$$${x}={e}^{{i}\frac{\pi}{\mathrm{3}{n}}\left(\mathrm{5}+\mathrm{6}{k}\right)\:} \:{or}\:\:{x}={e}^{{i}\frac{\pi}{\mathrm{3}{n}}\left(\mathrm{6}{k}+\mathrm{1}\right)} \:\:{with}\:{k}=\left(\mathrm{0},\mathrm{1},\mathrm{2},…,{n}−\mathrm{1}\right) \\ $$$$\left.\mathrm{2}\right) \\ $$$${p}\left({x}\right)=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left({x}−{e}^{{i}\frac{\pi}{\mathrm{3}{n}}\left(\mathrm{6}{k}+\mathrm{5}\right)} \right)\left({x}−{e}^{{i}\frac{\pi}{\mathrm{3}{n}}\left(\mathrm{6}{k}+\mathrm{1}\right)} \right) \\ $$$$\left.\mathrm{3}\right) \\ $$$${p}\left({x}\right)=\mathrm{0}\:{when}\:{x}={e}^{{i}\frac{\pi}{\mathrm{3}{n}}\left(\mathrm{6}{k}+\mathrm{5}\right)} \:{or}\:{x}={e}^{{i}\frac{\pi}{\mathrm{3}{n}}\left(\mathrm{6}{k}+\mathrm{1}\right)} \\ $$$${p}\left({x}\right)=\mathrm{2}\:\Leftrightarrow{x}^{\mathrm{2}{n}} −{x}^{{n}} +\mathrm{1}=\mathrm{2} \\ $$$${x}^{\mathrm{2}{n}} −{x}^{{n}} −\mathrm{1}=\mathrm{0} \\ $$$$\Delta=\mathrm{1}+\mathrm{4}=\mathrm{5} \\ $$$${x}^{{n}} =\frac{\mathrm{1}\underset{−} {+}\sqrt{\mathrm{5}}}{\mathrm{2}}={a} \\ $$$${x}=\sqrt[{{n}}]{{a}}{e}^{\frac{\mathrm{2}{ik}\pi}{{n}}} =\sqrt[{{n}}]{\frac{\mathrm{1}\underset{−} {+}\sqrt{\mathrm{5}}}{\mathrm{2}}}{e}^{\frac{\mathrm{2}{ik}\pi}{{n}}} \\ $$
Commented by afachri last updated on 08/Dec/18
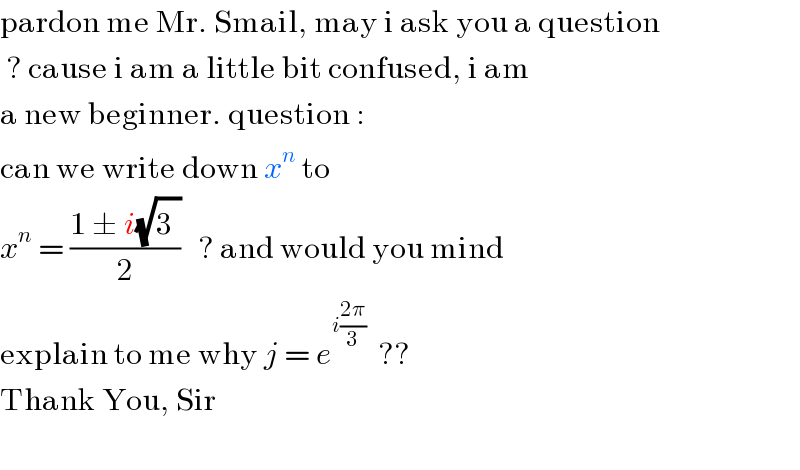
pardon me Mr. Smail, may i ask you a question ? cause i am a little bit confused, i am a new beginner. question : can we write down x^n to x^n = ((1 ± i(√3^ ))/2) ? and would you mind explain to me why j = e^(i((2π)/3)) ?? Thank You, Sir
$$\mathrm{pardon}\:\mathrm{me}\:\mathrm{Mr}.\:\mathrm{Smail},\:\mathrm{may}\:\mathrm{i}\:\mathrm{ask}\:\mathrm{you}\:\mathrm{a}\:\mathrm{question}\: \\ $$$$\:?\:\mathrm{cause}\:\mathrm{i}\:\mathrm{am}\:\mathrm{a}\:\mathrm{little}\:\mathrm{bit}\:\mathrm{confused},\:\mathrm{i}\:\mathrm{am} \\ $$$$\mathrm{a}\:\mathrm{new}\:\mathrm{beginner}.\:\mathrm{question}\:: \\ $$$$\mathrm{can}\:\mathrm{we}\:\mathrm{write}\:\mathrm{down}\:{x}^{{n}} \:\mathrm{to} \\ $$$${x}^{{n}} \:=\:\frac{\mathrm{1}\:\pm\:{i}\sqrt{\mathrm{3}^{} }}{\mathrm{2}}\:\:\:?\:\mathrm{and}\:\mathrm{would}\:\mathrm{you}\:\mathrm{mind}\: \\ $$$$\mathrm{explain}\:\mathrm{to}\:\mathrm{me}\:\mathrm{why}\:{j}\:=\:{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \:\:?? \\ $$$$\mathrm{Thank}\:\mathrm{You},\:\mathrm{Sir} \\ $$$$ \\ $$
Commented by Smail last updated on 08/Dec/18
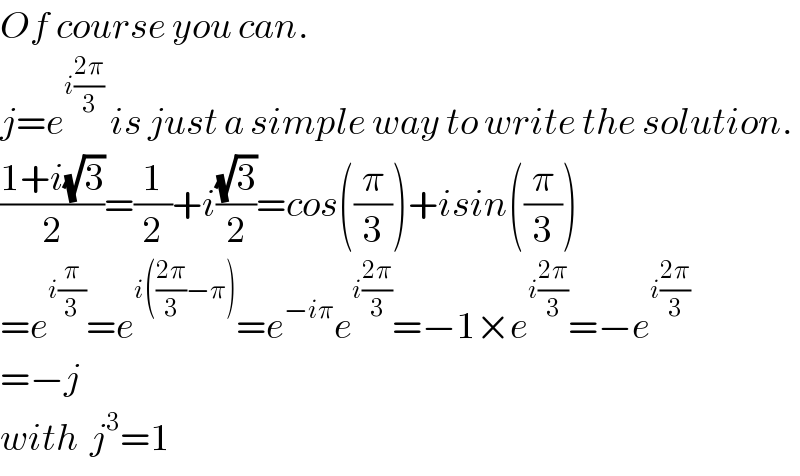
Of course you can. j=e^(i((2π)/3)) is just a simple way to write the solution. ((1+i(√3))/2)=(1/2)+i((√3)/2)=cos((π/3))+isin((π/3)) =e^(i(π/3)) =e^(i(((2π)/3)−π)) =e^(−iπ) e^(i((2π)/3)) =−1×e^(i((2π)/3)) =−e^(i((2π)/3)) =−j with j^3 =1
$${Of}\:{course}\:{you}\:{can}. \\ $$$${j}={e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \:{is}\:{just}\:{a}\:{simple}\:{way}\:{to}\:{write}\:{the}\:{solution}. \\ $$$$\frac{\mathrm{1}+{i}\sqrt{\mathrm{3}}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}+{i}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}={cos}\left(\frac{\pi}{\mathrm{3}}\right)+{isin}\left(\frac{\pi}{\mathrm{3}}\right) \\ $$$$={e}^{{i}\frac{\pi}{\mathrm{3}}} ={e}^{{i}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}−\pi\right)} ={e}^{−{i}\pi} {e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} =−\mathrm{1}×{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} =−{e}^{{i}\frac{\mathrm{2}\pi}{\mathrm{3}}} \\ $$$$=−{j} \\ $$$${with}\:\:{j}^{\mathrm{3}} =\mathrm{1} \\ $$
Commented by Smail last updated on 08/Dec/18
Also j^2 +j+1=0
$${Also}\:\:\:{j}^{\mathrm{2}} +{j}+\mathrm{1}=\mathrm{0} \\ $$
Commented by afachri last updated on 09/Dec/18
thank you sir, i got it. thank you very much :)
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{got}\:\mathrm{it}. \\ $$$$\left.\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\::\right) \\ $$
Commented by Smail last updated on 09/Dec/18
you are welcome
$${you}\:{are}\:{welcome} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *