Question Number 42098 by abdo.msup.com last updated on 17/Aug/18
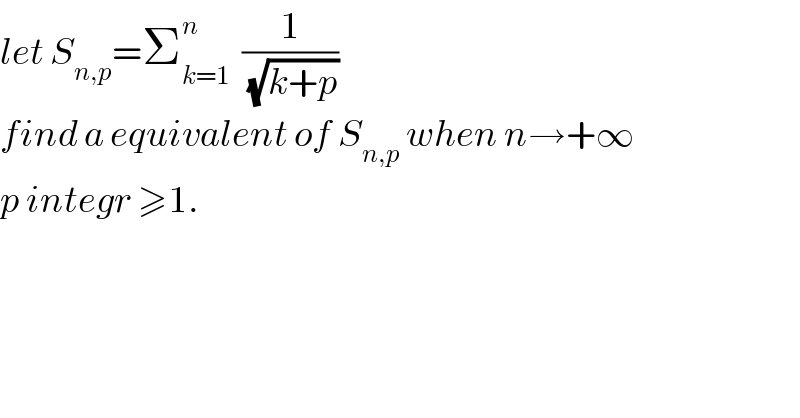
$${let}\:{S}_{{n},{p}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{1}}{\:\sqrt{{k}+{p}}} \\ $$$${find}\:{a}\:{equivalent}\:{of}\:{S}_{{n},{p}} \:{when}\:{n}\rightarrow+\infty \\ $$$${p}\:{integr}\:\geqslant\mathrm{1}. \\ $$
Commented by maxmathsup by imad last updated on 18/Aug/18
![the sequence ((1/( (√k))))_(k≥1) is decreasing ⇒ ∫_k ^(k+1) (dt/( (√(t+p)))) ≤ (1/( (√(k+p)))) ≤ ∫_(k−1) ^k (dt/( (√(t+p)))) ⇒ Σ_(k=1) ^n ∫_k ^(k+1) (dt/( (√(t+p)))) ≤Σ_(k=1) ^n (1/( (√(k+p)))) ≤ Σ_(k=1) ^n ∫_(k−1) ^k (dt/( (√(t+p)))) ⇒ ∫_1 ^(n+1) (dt/( (√(t+p)))) ≤ S_(n,p) ≤ ∫_0 ^n (dt/( (√(t+p)))) ⇒ [2(√(t+p))]_1 ^(n+1) ≤S_(n,p) ≤[2(√(t+p))]_0 ^n ⇒ 2(√(n+1+p)) −2(√(p+1)) ≤ S_(n,p) ≤ 2(√(n+p)) −2(√(p )) ⇒ ((2(√(n+1+p))−2(√(p+1)))/(2(√(n+p)))) ≤ (S_(n,p) /(2(√(n+p)))) ≤ ((2(√(n+p)) −2(√p))/(2(√(n+p)))) ⇒ (√(1+(1/(n+p))))−(√((p+1)/(n+p))) ≤ (S_(n,p) /(2(√(n+p)))) ≤ 1−(√(p/(n+p))) but lim_(n→+∞ ) (√(1+(1/(n+p))))−(√((p+1)/(n+1))) =1 and lim_(n→+∞) 1−(√(p/(n+p))) =1 ⇒ S_(n,p) ∼ 2(√(n+p)) (n→+∞ and p fixed)](https://www.tinkutara.com/question/Q42130.png)
$${the}\:{sequence}\:\left(\frac{\mathrm{1}}{\:\sqrt{{k}}}\right)_{{k}\geqslant\mathrm{1}} \:\:{is}\:{decreasing}\:\:\Rightarrow\:\:\int_{{k}} ^{{k}+\mathrm{1}} \:\:\frac{{dt}}{\:\sqrt{{t}+{p}}}\:\leqslant\:\frac{\mathrm{1}}{\:\sqrt{{k}+{p}}}\:\leqslant\:\int_{{k}−\mathrm{1}} ^{{k}} \:\frac{{dt}}{\:\sqrt{{t}+{p}}}\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \:\int_{{k}} ^{{k}+\mathrm{1}} \:\frac{{dt}}{\:\sqrt{{t}+{p}}}\:\leqslant\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\:\frac{\mathrm{1}}{\:\sqrt{{k}+{p}}}\:\leqslant\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\int_{{k}−\mathrm{1}} ^{{k}} \:\frac{{dt}}{\:\sqrt{{t}+{p}}}\:\Rightarrow \\ $$$$\int_{\mathrm{1}} ^{{n}+\mathrm{1}} \:\:\frac{{dt}}{\:\sqrt{{t}+{p}}}\:\leqslant\:{S}_{{n},{p}} \:\:\:\leqslant\:\int_{\mathrm{0}} ^{{n}} \:\:\frac{{dt}}{\:\sqrt{{t}+{p}}}\:\Rightarrow\:\left[\mathrm{2}\sqrt{{t}+{p}}\right]_{\mathrm{1}} ^{{n}+\mathrm{1}} \:\leqslant{S}_{{n},{p}} \:\leqslant\left[\mathrm{2}\sqrt{{t}+{p}}\right]_{\mathrm{0}} ^{{n}} \:\Rightarrow \\ $$$$\mathrm{2}\sqrt{{n}+\mathrm{1}+{p}}\:−\mathrm{2}\sqrt{{p}+\mathrm{1}}\:\leqslant\:{S}_{{n},{p}} \:\:\leqslant\:\mathrm{2}\sqrt{{n}+{p}}\:\:−\mathrm{2}\sqrt{{p}\:}\:\Rightarrow \\ $$$$\frac{\mathrm{2}\sqrt{{n}+\mathrm{1}+{p}}−\mathrm{2}\sqrt{{p}+\mathrm{1}}}{\mathrm{2}\sqrt{{n}+{p}}}\:\leqslant\:\:\:\frac{{S}_{{n},{p}} }{\mathrm{2}\sqrt{{n}+{p}}}\:\leqslant\:\:\frac{\mathrm{2}\sqrt{{n}+{p}}\:−\mathrm{2}\sqrt{{p}}}{\mathrm{2}\sqrt{{n}+{p}}}\:\Rightarrow \\ $$$$\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{n}+{p}}}−\sqrt{\frac{{p}+\mathrm{1}}{{n}+{p}}}\:\:\leqslant\:\:\frac{{S}_{{n},{p}} }{\mathrm{2}\sqrt{{n}+{p}}}\:\leqslant\:\:\mathrm{1}−\sqrt{\frac{{p}}{{n}+{p}}}\:\:\:{but} \\ $$$${lim}_{{n}\rightarrow+\infty\:} \sqrt{\mathrm{1}+\frac{\mathrm{1}}{{n}+{p}}}−\sqrt{\frac{{p}+\mathrm{1}}{{n}+\mathrm{1}}}\:=\mathrm{1}\:{and}\:{lim}_{{n}\rightarrow+\infty} \:\mathrm{1}−\sqrt{\frac{{p}}{{n}+{p}}}\:=\mathrm{1}\:\Rightarrow \\ $$$$\:\:\:{S}_{{n},{p}} \:\:\:\sim\:\:\mathrm{2}\sqrt{{n}+{p}}\:\:\:\:\left({n}\rightarrow+\infty\:\:{and}\:{p}\:{fixed}\right)\: \\ $$$$ \\ $$
