Question Number 87687 by ~blr237~ last updated on 05/Apr/20
![Let w=[1;(π/n)] ,n∈N^∗ a_n =Σ_(p=0) ^(n−1) ((2p+1)/(1−w^(2p+1) )) and b_n =Σ_(p=0) ^(n−1) (n/(1+w^p )) Find all integer n such as a_n =b_n](https://www.tinkutara.com/question/Q87687.png)
$${Let}\:\:{w}=\left[\mathrm{1};\frac{\pi}{{n}}\right]\:,{n}\in\mathbb{N}^{\ast} \: \\ $$$$\:{a}_{{n}} =\underset{{p}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\:\frac{\mathrm{2}{p}+\mathrm{1}}{\mathrm{1}−{w}^{\mathrm{2}{p}+\mathrm{1}} }\:\:\:\:{and}\:\:\:{b}_{{n}} =\underset{{p}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}\:\frac{{n}}{\mathrm{1}+{w}^{{p}} }\: \\ $$$${Find}\:\:{all}\:{integer}\:{n}\:{such}\:{as}\:\:{a}_{{n}} ={b}_{{n}} \: \\ $$
Answered by mind is power last updated on 05/Apr/20
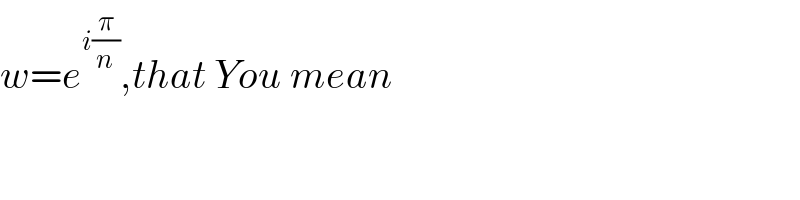
$${w}={e}^{{i}\frac{\pi}{{n}}} ,{that}\:{You}\:{mean} \\ $$
