Question Number 34736 by math khazana by abdo last updated on 10/May/18
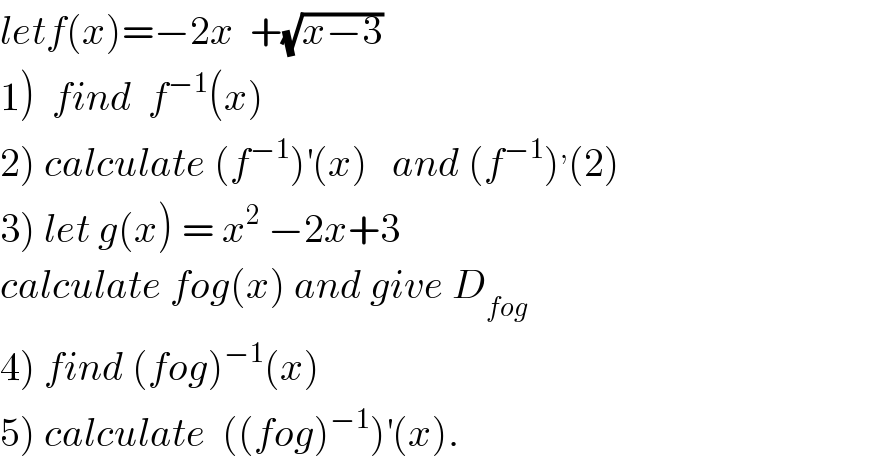
$${letf}\left({x}\right)=−\mathrm{2}{x}\:\:+\sqrt{{x}−\mathrm{3}} \\ $$$$\left.\mathrm{1}\right)\:\:{find}\:\:{f}^{−\mathrm{1}} \left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\left({f}^{−\mathrm{1}} \right)^{'} \left({x}\right)\:\:\:{and}\:\left({f}^{−\mathrm{1}} \right)^{,} \left(\mathrm{2}\right) \\ $$$$\left.\mathrm{3}\right)\:{let}\:{g}\left({x}\right)\:=\:{x}^{\mathrm{2}} \:−\mathrm{2}{x}+\mathrm{3} \\ $$$${calculate}\:{fog}\left({x}\right)\:{and}\:{give}\:{D}_{{fog}} \\ $$$$\left.\mathrm{4}\right)\:{find}\:\left({fog}\right)^{−\mathrm{1}} \left({x}\right) \\ $$$$\left.\mathrm{5}\right)\:{calculate}\:\:\left(\left({fog}\right)^{−\mathrm{1}} \right)^{'} \left({x}\right). \\ $$
Commented by prof Abdo imad last updated on 13/May/18
![D_f =[−3,+∞[ let put y=f(x) ⇔x=f^(−1) (y) y =f(x) ⇔ y=−2x +(√(x−3)) ⇔(y+2x)^2 =x−3 ⇒ y^2 +4yx +4x^2 −x+3=0 ⇒ 4x^2 +(4y−1)x +y^2 +3 =0 Δ = (4y−1)^2 −16(y^2 +3) = 16y^2 −8y +1 −16y^2 −48 =−8y −47 =−8(y +((47)/8)) Δ must be≥0 ⇒ y ≤ −((47)/8) and y +2x≥0 x_1 = ((1−4y +(√(−8y−47)))/8) x_2 = ((1−4y −(√(−8y−47)))/8) y +2x_1 = y +((1−4y +(√(−8y−47)))/4) =((1+(√(−8y−47)))/4)≥0 ⇒f^(−1) (x)= ((1−4x +(√(−8x−47)))/8) with Df^(−1) =]−∞,−((47)/8)] 2) (f^(−1) )^′ (x)= −(1/2) +(1/8) ((−8)/(2(√(−8x−47)))) =−(1/2) −(1/( (√(−8x−47)))) but 2 ∉ ]+∞,−((47)/8)[ so (f^(−1) )^′ (2) dont exist 3) we have f(x)=−2x +(√(x−3 )) and g(x)= x^2 −2x+3 ⇒ fog(x)=−2g(x)+(√(g(x)−3)) =−2x^2 +4x −6 +(√(x^2 −2x +3−3)) =−2x^2 +4x −6 +(√(x^2 −2x)) D_(fog ) =]−∞,0]∪[2,+∞[](https://www.tinkutara.com/question/Q34917.png)
$${D}_{{f}} =\left[−\mathrm{3},+\infty\left[\:{let}\:{put}\:{y}={f}\left({x}\right)\:\Leftrightarrow{x}={f}^{−\mathrm{1}} \left({y}\right)\right.\right. \\ $$$${y}\:={f}\left({x}\right)\:\Leftrightarrow\:{y}=−\mathrm{2}{x}\:+\sqrt{{x}−\mathrm{3}}\:\Leftrightarrow\left({y}+\mathrm{2}{x}\right)^{\mathrm{2}} \:={x}−\mathrm{3} \\ $$$$\Rightarrow\:{y}^{\mathrm{2}} \:+\mathrm{4}{yx}\:+\mathrm{4}{x}^{\mathrm{2}} \:−{x}+\mathrm{3}=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{4}{x}^{\mathrm{2}} \:\:+\left(\mathrm{4}{y}−\mathrm{1}\right){x}\:+{y}^{\mathrm{2}} \:+\mathrm{3}\:=\mathrm{0}\: \\ $$$$\Delta\:=\:\left(\mathrm{4}{y}−\mathrm{1}\right)^{\mathrm{2}} \:−\mathrm{16}\left({y}^{\mathrm{2}} +\mathrm{3}\right) \\ $$$$=\:\mathrm{16}{y}^{\mathrm{2}} \:\:−\mathrm{8}{y}\:+\mathrm{1}\:−\mathrm{16}{y}^{\mathrm{2}} \:\:−\mathrm{48}\:\:=−\mathrm{8}{y}\:−\mathrm{47} \\ $$$$=−\mathrm{8}\left({y}\:\:+\frac{\mathrm{47}}{\mathrm{8}}\right)\:\:\Delta\:{must}\:{be}\geqslant\mathrm{0}\:\:\Rightarrow\:{y}\:\leqslant\:−\frac{\mathrm{47}}{\mathrm{8}} \\ $$$${and}\:{y}\:+\mathrm{2}{x}\geqslant\mathrm{0}\:\:\:\:{x}_{\mathrm{1}} \:=\:\frac{\mathrm{1}−\mathrm{4}{y}\:+\sqrt{−\mathrm{8}{y}−\mathrm{47}}}{\mathrm{8}} \\ $$$${x}_{\mathrm{2}} =\:\frac{\mathrm{1}−\mathrm{4}{y}\:−\sqrt{−\mathrm{8}{y}−\mathrm{47}}}{\mathrm{8}} \\ $$$${y}\:+\mathrm{2}{x}_{\mathrm{1}} \:=\:{y}\:\:\:+\frac{\mathrm{1}−\mathrm{4}{y}\:+\sqrt{−\mathrm{8}{y}−\mathrm{47}}}{\mathrm{4}} \\ $$$$=\frac{\mathrm{1}+\sqrt{−\mathrm{8}{y}−\mathrm{47}}}{\mathrm{4}}\geqslant\mathrm{0}\:\Rightarrow{f}^{−\mathrm{1}} \left({x}\right)=\:\frac{\mathrm{1}−\mathrm{4}{x}\:+\sqrt{−\mathrm{8}{x}−\mathrm{47}}}{\mathrm{8}} \\ $$$$\left.{w}\left.{ith}\:{Df}^{−\mathrm{1}} \:\:\:=\right]−\infty,−\frac{\mathrm{47}}{\mathrm{8}}\right] \\ $$$$\left.\mathrm{2}\right)\:\left({f}^{−\mathrm{1}} \right)^{'} \left({x}\right)=\:−\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{8}}\:\frac{−\mathrm{8}}{\mathrm{2}\sqrt{−\mathrm{8}{x}−\mathrm{47}}} \\ $$$$\left.=−\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\:\sqrt{−\mathrm{8}{x}−\mathrm{47}}}\:\:\:\:\:{but}\:\mathrm{2}\:\notin\:\right]+\infty,−\frac{\mathrm{47}}{\mathrm{8}}\left[\:{so}\right. \\ $$$$\left({f}^{−\mathrm{1}} \right)^{'} \left(\mathrm{2}\right)\:{dont}\:{exist} \\ $$$$\left.\mathrm{3}\right)\:{we}\:{have}\:{f}\left({x}\right)=−\mathrm{2}{x}\:+\sqrt{{x}−\mathrm{3}\:}\:\:\:{and} \\ $$$${g}\left({x}\right)=\:{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{3}\:\Rightarrow \\ $$$${fog}\left({x}\right)=−\mathrm{2}{g}\left({x}\right)+\sqrt{{g}\left({x}\right)−\mathrm{3}} \\ $$$$=−\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{4}{x}\:−\mathrm{6}\:\:+\sqrt{{x}^{\mathrm{2}} \:−\mathrm{2}{x}\:+\mathrm{3}−\mathrm{3}} \\ $$$$=−\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{4}{x}\:−\mathrm{6}\:\:+\sqrt{{x}^{\mathrm{2}} \:−\mathrm{2}{x}} \\ $$$$\left.{D}_{{fog}\:} \left.=\right]−\infty,\mathrm{0}\right]\cup\left[\mathrm{2},+\infty\left[\right.\right. \\ $$
