Menu Close

lim-x-0-1-x-2-x-n-x-n-1-x-

Tinku Tara 0 Comments
Pin




Question Number 164705 by Kayela last updated on 20/Jan/22
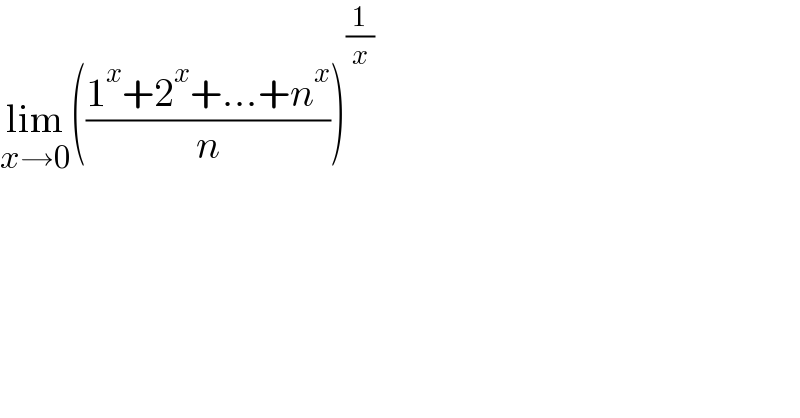
lim_(x→0) (((1^x +2^x +...+n^x )/n))^(1/x)
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}^{{x}} +\mathrm{2}^{{x}} +…+{n}^{{x}} }{{n}}\right)^{\frac{\mathrm{1}}{{x}}} \\ $$
Answered by Berlindo last updated on 20/Jan/22
=[lim_(x→0) (1+((1^x +2^x +...+n^x −n)/n))^(n/(1^x +2^x +...+n^x −n)) ]^(lim_(x→0) ((1^x +2^x +...+n^x −n)/x)∙(1/n)) =e^(lim_(x→0) (((1^x −1)+(2^x −1)+...+(n^x −1))/x)∙(1/n)) =e^([lim_(x→0) ((1^x −1)/x)+lim_(x→0) ((2^x −1)/x)+...+lim_(x→0) ((n^x −1)/x)]∙(1/n)) =e^((ln 1+ln 2+...+ln n)∙(1/n)) =e^((1/n)ln (n!)) =e^(ln (((n!))^(1/n) )) =((n!))^(1/n) ∴lim_(x→0) (((1^x +2^x +...+n^x )/n))^(1/x) =((n!))^(1/n) ★Berlindo Ndala★
$$=\left[\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{1}^{\mathrm{x}} +\mathrm{2}^{\mathrm{x}} +…+\mathrm{n}^{\mathrm{x}} −\mathrm{n}}{\mathrm{n}}\right)^{\frac{\mathrm{n}}{\mathrm{1}^{\mathrm{x}} +\mathrm{2}^{\mathrm{x}} +…+\mathrm{n}^{\mathrm{x}} −\mathrm{n}}} \right]^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}^{\mathrm{x}} +\mathrm{2}^{\mathrm{x}} +…+\mathrm{n}^{\mathrm{x}} −\mathrm{n}}{\mathrm{x}}\centerdot\frac{\mathrm{1}}{\mathrm{n}}} \\ $$$$=\mathrm{e}^{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\left(\mathrm{1}^{\mathrm{x}} −\mathrm{1}\right)+\left(\mathrm{2}^{\mathrm{x}} −\mathrm{1}\right)+…+\left(\mathrm{n}^{\mathrm{x}} −\mathrm{1}\right)}{\mathrm{x}}\centerdot\frac{\mathrm{1}}{\mathrm{n}}} \\ $$$$=\mathrm{e}^{\left[\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}^{\mathrm{x}} −\mathrm{1}}{\mathrm{x}}+\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}^{\mathrm{x}} −\mathrm{1}}{\mathrm{x}}+…+\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{n}^{\mathrm{x}} −\mathrm{1}}{\mathrm{x}}\right]\centerdot\frac{\mathrm{1}}{\mathrm{n}}} \\ $$$$=\mathrm{e}^{\left(\mathrm{ln}\:\mathrm{1}+\mathrm{ln}\:\mathrm{2}+…+\mathrm{ln}\:\mathrm{n}\right)\centerdot\frac{\mathrm{1}}{\mathrm{n}}} =\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{n}}\mathrm{ln}\:\left(\mathrm{n}!\right)} =\mathrm{e}^{\mathrm{ln}\:\left(\sqrt[{\mathrm{n}}]{\mathrm{n}!}\right)} \\ $$$$=\sqrt[{\mathrm{n}}]{\mathrm{n}!} \\ $$$$\therefore\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}^{{x}} +\mathrm{2}^{{x}} +…+{n}^{{x}} }{{n}}\right)^{\frac{\mathrm{1}}{{x}}} =\sqrt[{\mathrm{n}}]{\mathrm{n}!} \\ $$$$\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\bigstar\mathrm{Berlindo}\:\mathrm{Ndala}\bigstar \\ $$
Answered by puissant last updated on 21/Jan/22
=lim_(x→0) (((e^(xln1) +e^(xln2) +...+e^(xlnn) )/n))^(1/x) =lim_(x→0) ((((1+xln1)+(1+xln2)+...+(1+xlnn))/n))^(1/x) =lim_(x→0) (1+((xln(n!))/n))^(1/x) = lim_(x→0) e^((1/x)ln(1+((xln(n!))/n))) = lim_(x→0) e^((1/x)(((xln(n!))/n))) = e^(((ln(n!))/n) ) = ((n!))^(1/n) .. ............Le puissant...........
$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{{e}^{{xln}\mathrm{1}} +{e}^{{xln}\mathrm{2}} +…+{e}^{{xlnn}} }{{n}}\right)^{\frac{\mathrm{1}}{{x}}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\left(\mathrm{1}+{xln}\mathrm{1}\right)+\left(\mathrm{1}+{xln}\mathrm{2}\right)+…+\left(\mathrm{1}+{xlnn}\right)}{{n}}\right)^{\frac{\mathrm{1}}{{x}}} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\mathrm{1}+\frac{{xln}\left({n}!\right)}{{n}}\right)^{\frac{\mathrm{1}}{{x}}} \\ $$$$=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{e}^{\frac{\mathrm{1}}{{x}}{ln}\left(\mathrm{1}+\frac{{xln}\left({n}!\right)}{{n}}\right)} \:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{e}^{\frac{\mathrm{1}}{{x}}\left(\frac{{xln}\left({n}!\right)}{{n}}\right)} \\ $$$$=\:{e}^{\frac{{ln}\left({n}!\right)}{{n}}\:} =\:\sqrt[{{n}}]{{n}!}.. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:…………\mathscr{L}{e}\:{puissant}………..\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *