Question Number 79181 by naka3546 last updated on 23/Jan/20
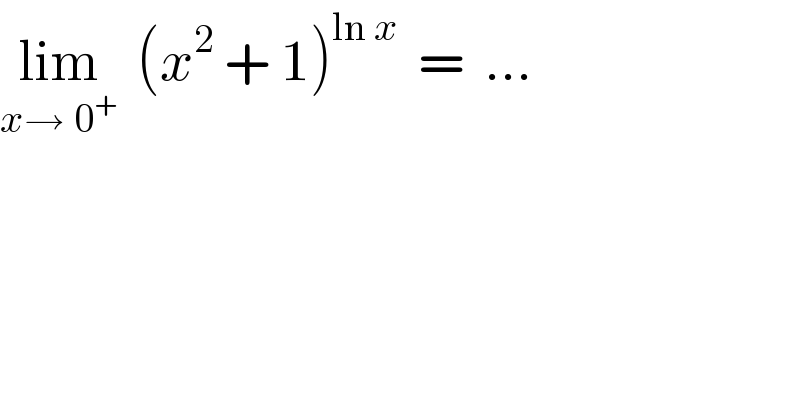
$$\underset{{x}\rightarrow\:\mathrm{0}^{+} } {\mathrm{lim}}\:\:\left({x}^{\mathrm{2}} \:+\:\mathrm{1}\right)^{\mathrm{ln}\:{x}} \:\:=\:\:… \\ $$
Commented by john santu last updated on 23/Jan/20
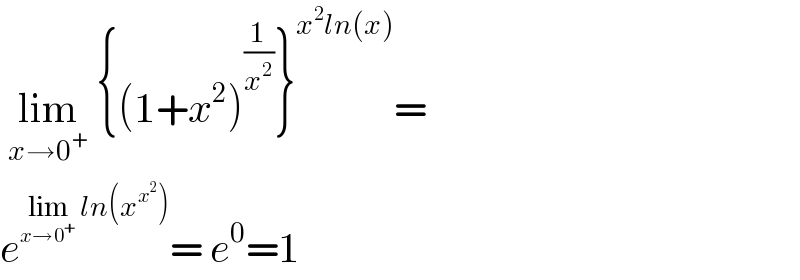
$$\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\left\{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{{x}^{\mathrm{2}} }} \right\}^{{x}^{\mathrm{2}} {ln}\left({x}\right)} = \\ $$$${e}^{\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:{ln}\left({x}^{{x}^{\mathrm{2}} } \right)} =\:{e}^{\mathrm{0}} =\mathrm{1} \\ $$
Answered by MJS last updated on 23/Jan/20
![lim_(x→0^+ ) (ln x ln (x^2 +1)) =lim_(x→0^+ ) ((ln (x^2 +1))/(1/(ln x))) = [L′Hospital] =lim_(x→0^+ ) (((2x)/(x^2 +1))/(−(1/(x(ln x)^2 ))))=−2lim_(x→0^+ ) (((xln x)^2 )/(x^2 +1)) =0 ⇒ lim_(x→0^+ ) (x^2 +1)^(ln x) =1](https://www.tinkutara.com/question/Q79185.png)
$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\left(\mathrm{ln}\:{x}\:\mathrm{ln}\:\left({x}^{\mathrm{2}} +\mathrm{1}\right)\right)\:=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\mathrm{ln}\:\left({x}^{\mathrm{2}} +\mathrm{1}\right)}{\frac{\mathrm{1}}{\mathrm{ln}\:{x}}}\:= \\ $$$$\:\:\:\:\:\left[\mathrm{L}'\mathrm{Hospital}\right] \\ $$$$=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}}{−\frac{\mathrm{1}}{{x}\left(\mathrm{ln}\:{x}\right)^{\mathrm{2}} }}=−\mathrm{2}\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\left({x}\mathrm{ln}\:{x}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} +\mathrm{1}}\:=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{ln}\:{x}} \:=\mathrm{1} \\ $$
