Question Number 95323 by ~blr237~ last updated on 24/May/20
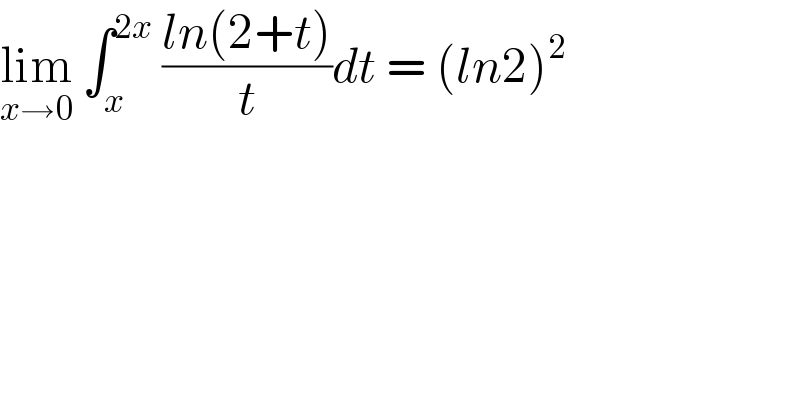
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\int_{{x}} ^{\mathrm{2}{x}} \:\frac{{ln}\left(\mathrm{2}+{t}\right)}{{t}}{dt}\:=\:\left({ln}\mathrm{2}\right)^{\mathrm{2}} \\ $$
Answered by abdomathmax last updated on 24/May/20
![∃ c∈]x,2x[ / ∫_x ^(2x) ((ln(2+t))/t)dt =ln(2+c)∫_x ^(2x) (dt/t) =ln(2+c)ln(((2x)/x)) (x→0 ⇒c→0 ⇒ lim_(x→0) ∫_x ^(2x) ((ln(2+t))/t)dt =ln(2).ln(2) =(ln2)^2](https://www.tinkutara.com/question/Q95338.png)
$$\left.\exists\:\mathrm{c}\in\right]\mathrm{x},\mathrm{2x}\left[\:/\:\int_{\mathrm{x}} ^{\mathrm{2x}} \:\frac{\mathrm{ln}\left(\mathrm{2}+\mathrm{t}\right)}{\mathrm{t}}\mathrm{dt}\:=\mathrm{ln}\left(\mathrm{2}+\mathrm{c}\right)\int_{\mathrm{x}} ^{\mathrm{2x}} \:\frac{\mathrm{dt}}{\mathrm{t}}\right. \\ $$$$=\mathrm{ln}\left(\mathrm{2}+\mathrm{c}\right)\mathrm{ln}\left(\frac{\mathrm{2x}}{\mathrm{x}}\right)\:\:\:\left(\mathrm{x}\rightarrow\mathrm{0}\:\Rightarrow\mathrm{c}\rightarrow\mathrm{0}\:\Rightarrow\right. \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \:\int_{\mathrm{x}} ^{\mathrm{2x}} \:\frac{\mathrm{ln}\left(\mathrm{2}+\mathrm{t}\right)}{\mathrm{t}}\mathrm{dt}\:=\mathrm{ln}\left(\mathrm{2}\right).\mathrm{ln}\left(\mathrm{2}\right)\:=\left(\mathrm{ln2}\right)^{\mathrm{2}} \\ $$
