Question Number 148849 by EDWIN88 last updated on 31/Jul/21
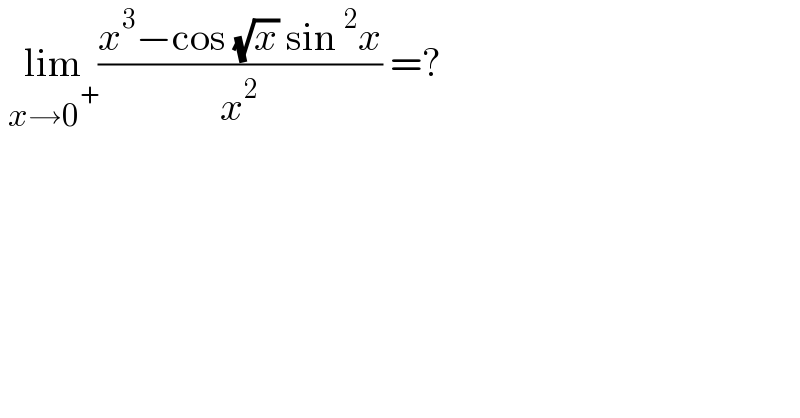
$$\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{{x}^{\mathrm{3}} −\mathrm{cos}\:\sqrt{{x}}\:\mathrm{sin}\:^{\mathrm{2}} {x}}{{x}^{\mathrm{2}} }\:=? \\ $$
Answered by iloveisrael last updated on 01/Aug/21
![lim_(x→0^+ ) ((x^3 −sin^3 x+sin^3 x−cos (√x) sin^2 x)/x^2 ) =lim_(x→0^+ ) ((x^3 −sin^3 x)/x^2 )+lim_(x→0^+ ) ((sin^2 x(sin x−cos (√x)))/x^2 ) =lim_(x→0^+ ) (((x−sin x)(x^2 +x sin x+sin^2 x))/x^2 )+lim_(x→0^+ ) (sin x−cos (√x) ) =lim_(x→0^+ ) (((((x−sin x)/x^3 )). x^3 (x^2 +x sin x+sin^2 x))/x^2 )−1 =lim_(x→0) (((1/6)x^3 (x^2 +x sin x+sin^2 x))/x^2 )−1 =(1/6)[lim_(x→0^+ ) (x(x^2 +x sin x+sin^2 x)]−1= −1.](https://www.tinkutara.com/question/Q148870.png)
$$\:\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\mathrm{x}^{\mathrm{3}} −\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}+\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}−\mathrm{cos}\:\sqrt{\mathrm{x}}\:\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\mathrm{x}^{\mathrm{3}} −\mathrm{sin}\:^{\mathrm{3}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} }+\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\left(\mathrm{sin}\:\mathrm{x}−\mathrm{cos}\:\sqrt{\mathrm{x}}\right)}{\mathrm{x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\left(\mathrm{x}−\mathrm{sin}\:\mathrm{x}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\:\mathrm{sin}\:\mathrm{x}+\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} }+\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left(\mathrm{sin}\:\mathrm{x}−\mathrm{cos}\:\sqrt{\mathrm{x}}\:\right) \\ $$$$=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\left(\frac{\mathrm{x}−\mathrm{sin}\:\mathrm{x}}{\mathrm{x}^{\mathrm{3}} }\right).\:\mathrm{x}^{\mathrm{3}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\:\mathrm{sin}\:\mathrm{x}+\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} }−\mathrm{1} \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\frac{\mathrm{1}}{\mathrm{6}}\mathrm{x}^{\mathrm{3}} \left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\:\mathrm{sin}\:\mathrm{x}+\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} }−\mathrm{1} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left[\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\left(\mathrm{x}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}\:\mathrm{sin}\:\mathrm{x}+\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}\right)\right]−\mathrm{1}=\:−\mathrm{1}.\:\right. \\ $$
Answered by mathmax by abdo last updated on 01/Aug/21
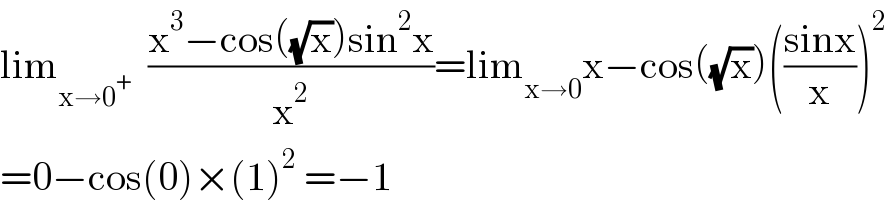
$$\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}^{+} } \:\:\frac{\mathrm{x}^{\mathrm{3}} −\mathrm{cos}\left(\sqrt{\mathrm{x}}\right)\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{x}^{\mathrm{2}} }=\mathrm{lim}_{\mathrm{x}\rightarrow\mathrm{0}} \mathrm{x}−\mathrm{cos}\left(\sqrt{\mathrm{x}}\right)\left(\frac{\mathrm{sinx}}{\mathrm{x}}\right)^{\mathrm{2}} \\ $$$$=\mathrm{0}−\mathrm{cos}\left(\mathrm{0}\right)×\left(\mathrm{1}\right)^{\mathrm{2}} \:=−\mathrm{1} \\ $$
