Question Number 170057 by nimnim last updated on 15/May/22
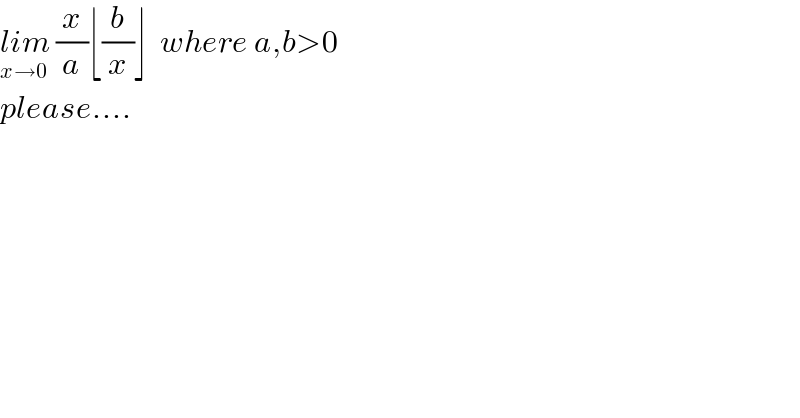
$$\underset{{x}\rightarrow\mathrm{0}} {{lim}}\:\frac{{x}}{{a}}\lfloor\frac{{b}}{{x}}\rfloor\:\:{where}\:{a},{b}>\mathrm{0} \\ $$$${please}…. \\ $$
Answered by mahdipoor last updated on 15/May/22
![get (b/x)=t lim_(x→0) (x/a)[(b/x)]=lim_(x→0) (b/a)×(([(b/x)])/(b/x))=(b/a)lim_(t→±∞) (([t])/t)=(b/a)](https://www.tinkutara.com/question/Q170063.png)
$${get}\:\frac{{b}}{{x}}={t}\:\: \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}}{{a}}\left[\frac{{b}}{{x}}\right]=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{b}}{{a}}×\frac{\left[\frac{{b}}{{x}}\right]}{\frac{{b}}{{x}}}=\frac{{b}}{{a}}\underset{{t}\rightarrow\pm\infty} {\mathrm{lim}}\frac{\left[{t}\right]}{{t}}=\frac{{b}}{{a}} \\ $$
