Question Number 169291 by infinityaction last updated on 28/Apr/22
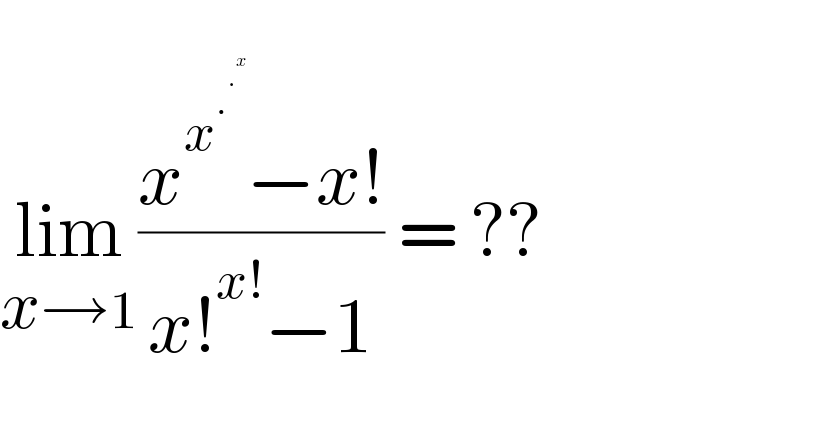
$$ \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{x}^{{x}^{.^{.^{{x}} } } } −{x}!}{{x}!^{{x}!} −\mathrm{1}}\:=\:?? \\ $$$$ \\ $$
Commented by infinityaction last updated on 28/Apr/22

$${please}\:{solve}\:{this}\:{problem} \\ $$
Commented by infinityaction last updated on 30/Apr/22
![{let}y = x^x^.^.^x x→1 then y → 1 log y = x^y ⇒ (dy/dx) = (y^2 /(x(1−log y))) t = x!^(x! ) ⇒ (dt/dx) = (x!^(x!) )′ = ((dx!)/dx)+log (x!)×((dx!)/dx) Use L−Hospital Rule In This Question {let}p =lim_( (x_( ) ,y)→1) (((x^y )′−(x!)^′ )/((x!)^′ −0)) p = lim_((x,y)→1) [ (((y^2 /(x1−log y)))−(x!)′)/(((dx!)/dx)+(log x!)×((dx!)/dx)))] p = (x!)′ = (⌈x+1)′ = x!(−γ+Σ_(k=1) ^x (1/k)) p = (x!)_(x=1) ^′ = (⌈x+1)_(x=1) ^′ = 1−γ p = (({1−(−γ+1)})/(1−γ + 0×(1−γ))) p = (𝛄/(1−𝛄))](https://www.tinkutara.com/question/Q169297.png)
$$ \\ $$$$\:\:\:\left\{\mathrm{let}\right\}{y}\:=\:\boldsymbol{{x}}^{\boldsymbol{{x}}^{.^{.^{\boldsymbol{{x}}} } } } \\ $$$$\:\:\:\:\:\:\:{x}\rightarrow\mathrm{1}\:{then}\:\:\:{y}\:\rightarrow\:\mathrm{1} \\ $$$$\:\:\:\:\:\:\mathrm{log}\:{y}\:=\:{x}^{{y}} \:\Rightarrow\:\frac{{dy}}{{dx}}\:=\:\frac{{y}^{\mathrm{2}} }{{x}\left(\mathrm{1}−\mathrm{log}\:{y}\right)} \\ $$$$\:\:\:\:\:{t}\:\:=\:{x}!^{{x}!\:} \Rightarrow\:\frac{{dt}}{{dx}}\:=\:\left({x}!^{{x}!} \right)'\:=\:\frac{{dx}!}{{dx}}+\mathrm{log}\:\left({x}!\right)×\frac{{dx}!}{{dx}} \\ $$$$\:\:\:\:\:\mathrm{Use}\:\mathrm{L}−\mathrm{Hospital}\:\mathrm{Rule}\:\mathrm{In}\:\mathrm{This}\:\mathrm{Question} \\ $$$$\:\:\:\:\:\left\{{let}\right\}{p}\:\:\:=\underset{\:\:\:\:\:\:\:\:\left(\underset{\:\:\:\:\:} {{x}},{y}\right)\rightarrow\mathrm{1}} {\mathrm{lim}}\:\frac{\left({x}^{{y}} \right)'−\left({x}!\right)^{'} }{\left({x}!\right)^{'} −\mathrm{0}} \\ $$$$\:\:\:\:\:\:\:\:\:{p}\:\:\:=\:\:\underset{\left({x},{y}\right)\rightarrow\mathrm{1}} {\mathrm{lim}}\left[\:\frac{\frac{{y}^{\mathrm{2}} }{\left.{x}\mathrm{1}−\mathrm{log}\:{y}\right)}−\left({x}!\right)'}{\frac{{dx}!}{{dx}}+\left(\mathrm{log}\:{x}!\right)×\frac{{dx}!}{{dx}}}\right] \\ $$$$\:\:\:\:\:\:\:{p}\:\:=\:\left({x}!\right)'\:=\:\left(\lceil{x}+\mathrm{1}\right)'\:=\:{x}!\left(−\gamma+\underset{{k}=\mathrm{1}} {\overset{{x}} {\sum}}\frac{\mathrm{1}}{{k}}\right) \\ $$$$\:\:\:\:\:\boldsymbol{{p}}\:\:=\:\:\left(\boldsymbol{{x}}!\right)_{\boldsymbol{{x}}=\mathrm{1}} ^{'} \:=\:\left(\lceil\boldsymbol{{x}}+\mathrm{1}\right)_{\boldsymbol{{x}}=\mathrm{1}} ^{'} =\:\mathrm{1}−\gamma \\ $$$$\:\:\:\:\:\:{p}\:\:\:\:\:\:=\:\:\:\frac{\left\{\mathrm{1}−\left(−\gamma+\mathrm{1}\right)\right\}}{\mathrm{1}−\gamma\:+\:\mathrm{0}×\left(\mathrm{1}−\gamma\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\boldsymbol{{p}}\:\:=\:\:\frac{\boldsymbol{\gamma}}{\mathrm{1}−\boldsymbol{\gamma}} \\ $$$$ \\ $$$$ \\ $$
Commented by infinityaction last updated on 28/Apr/22
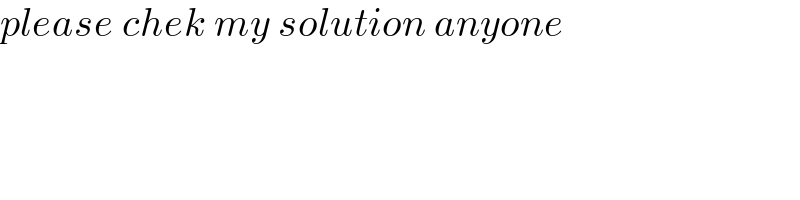
$${please}\:{chek}\:{my}\:{solution}\:{anyone} \\ $$
Commented by infinityaction last updated on 28/Apr/22

$$\boldsymbol{{mr}}\:\boldsymbol{{w}}\:{and}\:\boldsymbol{{qaz}}\:{sir}\:{please}\:{chek}\:{my}\:{solution} \\ $$$${right}\:{or}\:{wrong}\:?? \\ $$
Commented by qaz last updated on 29/Apr/22
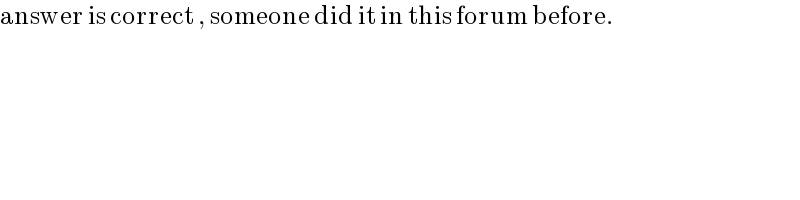
$$\mathrm{answer}\:\mathrm{is}\:\mathrm{correct}\:,\:\mathrm{someone}\:\mathrm{did}\:\mathrm{it}\:\mathrm{in}\:\mathrm{this}\:\mathrm{forum}\:\mathrm{before}. \\ $$
Commented by infinityaction last updated on 30/Apr/22
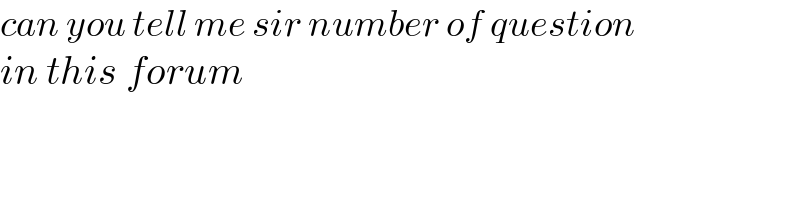
$${can}\:{you}\:{tell}\:{me}\:{sir}\:{number}\:{of}\:{question} \\ $$$${in}\:{this}\:{forum} \\ $$
