Question Number 15195 by Joel577 last updated on 08/Jun/17
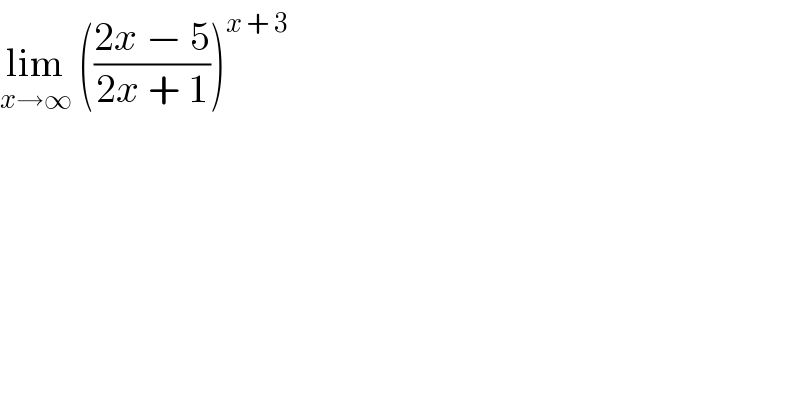
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{\mathrm{2}{x}\:−\:\mathrm{5}}{\mathrm{2}{x}\:+\:\mathrm{1}}\right)^{{x}\:+\:\mathrm{3}} \\ $$
Commented by Joel577 last updated on 08/Jun/17
![= lim_(x→∞) (1 − (6/(2x + 1)))^(x + 3) = lim_(x→∞) {[(1 − (6/(2x + 1)))^(− ((2x + 1)/6)) ]^(− (6/(2x + 1))) }^(x + 3) = [ lim_(x→∞) (1 − (6/(2x + 1)))^(− ((2x + 1)/6)) ]^(lim_(x→∞) (−((6(x + 3))/(2x + 1)))) = e^(−3) Is it correct?](https://www.tinkutara.com/question/Q15198.png)
$$=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{1}\:−\:\frac{\mathrm{6}}{\mathrm{2}{x}\:+\:\mathrm{1}}\right)^{{x}\:+\:\mathrm{3}} \\ $$$$=\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left\{\left[\left(\mathrm{1}\:−\:\frac{\mathrm{6}}{\mathrm{2}{x}\:+\:\mathrm{1}}\right)^{−\:\frac{\mathrm{2}{x}\:+\:\mathrm{1}}{\mathrm{6}}} \right]^{−\:\frac{\mathrm{6}}{\mathrm{2}{x}\:+\:\mathrm{1}}} \right\}^{{x}\:+\:\mathrm{3}} \\ $$$$=\:\left[\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{1}\:−\:\frac{\mathrm{6}}{\mathrm{2}{x}\:+\:\mathrm{1}}\right)^{−\:\frac{\mathrm{2}{x}\:+\:\mathrm{1}}{\mathrm{6}}} \right]^{\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(−\frac{\mathrm{6}\left({x}\:+\:\mathrm{3}\right)}{\mathrm{2}{x}\:+\:\mathrm{1}}\right)} \\ $$$$=\:{e}^{−\mathrm{3}} \\ $$$$ \\ $$$$\mathrm{Is}\:\mathrm{it}\:\mathrm{correct}? \\ $$
Commented by Joel577 last updated on 08/Jun/17
$${thank}\:{you}\:{very}\:{much} \\ $$
Commented by mrW1 last updated on 08/Jun/17

$$\mathrm{correct}! \\ $$
