Question Number 123375 by bemath last updated on 25/Nov/20
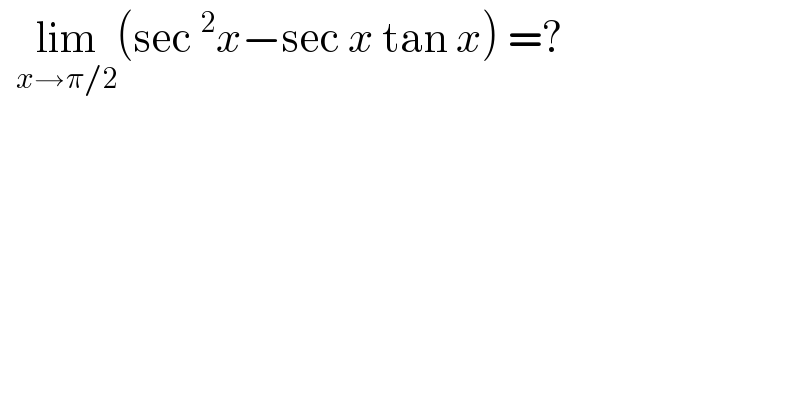
$$\:\:\underset{{x}\rightarrow\pi/\mathrm{2}} {\mathrm{lim}}\left(\mathrm{sec}\:^{\mathrm{2}} {x}−\mathrm{sec}\:{x}\:\mathrm{tan}\:{x}\right)\:=? \\ $$
Answered by Dwaipayan Shikari last updated on 25/Nov/20
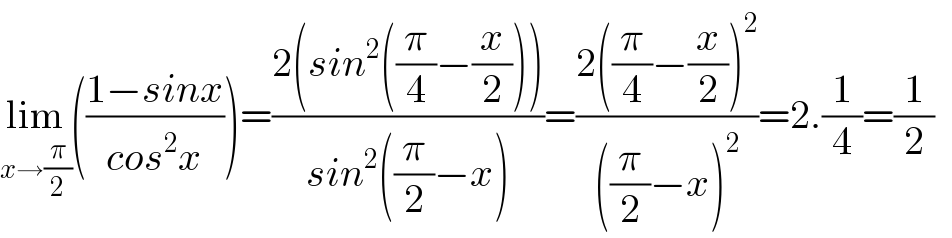
$$\underset{{x}\rightarrow\frac{\pi}{\mathrm{2}}} {\mathrm{lim}}\left(\frac{\mathrm{1}−{sinx}}{{cos}^{\mathrm{2}} {x}}\right)=\frac{\mathrm{2}\left({sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)\right)}{{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}}−{x}\right)}=\frac{\mathrm{2}\left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} }{\left(\frac{\pi}{\mathrm{2}}−{x}\right)^{\mathrm{2}} }=\mathrm{2}.\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}}\:\: \\ $$
Answered by liberty last updated on 25/Nov/20
![lim_(x→π/2) sec x(sec x−tan x)= lim_(x→π/2) (((((1−sin x)/(cos x))))/(cos x)) = lim_(x→π/2) ((1−sin x)/(cos^2 x)) [ let x=(π/2)+y ; y→0 ] lim_(y→0) ((1−cos y)/(sin^2 y)) = lim_(y→0) ((2sin^2 (y/2))/(sin^2 y))=(1/2)](https://www.tinkutara.com/question/Q123383.png)
$$\:\:\underset{{x}\rightarrow\pi/\mathrm{2}} {\mathrm{lim}sec}\:{x}\left(\mathrm{sec}\:{x}−\mathrm{tan}\:{x}\right)= \\ $$$$\:\underset{{x}\rightarrow\pi/\mathrm{2}} {\mathrm{lim}}\:\frac{\left(\frac{\mathrm{1}−\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}}\right)}{\mathrm{cos}\:{x}}\:=\:\underset{{x}\rightarrow\pi/\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{sin}\:{x}}{\mathrm{cos}\:^{\mathrm{2}} {x}} \\ $$$$\:\left[\:{let}\:{x}=\frac{\pi}{\mathrm{2}}+{y}\:;\:{y}\rightarrow\mathrm{0}\:\right]\: \\ $$$$\:\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}\:{y}}{\mathrm{sin}\:^{\mathrm{2}} {y}}\:=\:\underset{{y}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2sin}\:^{\mathrm{2}} \left({y}/\mathrm{2}\right)}{\mathrm{sin}\:^{\mathrm{2}} {y}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
