Question Number 172913 by cortano1 last updated on 03/Jul/22
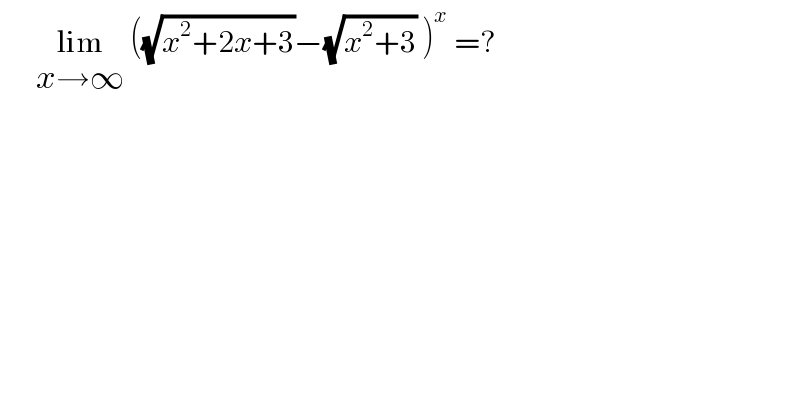
$$\:\:\:\:\:\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\left(\sqrt{{x}^{\mathrm{2}} +\mathrm{2}{x}+\mathrm{3}}−\sqrt{{x}^{\mathrm{2}} +\mathrm{3}}\:\right)^{{x}} \:=? \\ $$
Answered by FongXD last updated on 03/Jul/22
![=lim_(x→+∞) (((2x)/( (√(x^2 +2x+3))+(√(x^2 +3)))))^x =lim_(x→+∞) ((2/( (√(1+(2/x)+(3/x^2 )))+(√(1+(3/x^2 ))))))^x put t=(1/x), x→+∞, ⇒ t→0 =lim_(t→0) ((2/( (√(1+2t+3t^2 ))+(√(1+3t^2 )))))^(1/t) =lim_(t→0) [(1+((2−(√(1+2t+3t^2 ))−(√(1+3t^2 )))/( (√(1+2t+3t^2 ))+(√(1+3t^2 )))))^(1/□) ]^(□/t) =e^(lim_(t→0) ((2−(√(1+2t+3t^2 ))−(√(1+3t^2 )))/( ((√(1+2t+3t^2 ))+(√(1+3t^2 )))t))) =e^((1/2)lim_(t→0) (((1−(√(1+2t+3t^2 )))/t)+((1−(√(1+3t^2 )))/t))) =e^((1/2)lim_(t→0) (((−2−3t)/(1+(√(1+2t+3t^2 ))))−((3t)/( 1+(√(1+3t^2 )))))) =e^(−(1/2)) =(1/( (√e)))](https://www.tinkutara.com/question/Q172922.png)
$$=\underset{\mathrm{x}\rightarrow+\infty} {\mathrm{lim}}\left(\frac{\mathrm{2x}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{3}}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{3}}}\right)^{\mathrm{x}} \\ $$$$=\underset{\mathrm{x}\rightarrow+\infty} {\mathrm{lim}}\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{2}}{\mathrm{x}}+\frac{\mathrm{3}}{\mathrm{x}^{\mathrm{2}} }}+\sqrt{\mathrm{1}+\frac{\mathrm{3}}{\mathrm{x}^{\mathrm{2}} }}}\right)^{\mathrm{x}} \\ $$$$\mathrm{put}\:\mathrm{t}=\frac{\mathrm{1}}{\mathrm{x}},\:\mathrm{x}\rightarrow+\infty,\:\Rightarrow\:\mathrm{t}\rightarrow\mathrm{0} \\ $$$$=\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}+\mathrm{2t}+\mathrm{3t}^{\mathrm{2}} }+\sqrt{\mathrm{1}+\mathrm{3t}^{\mathrm{2}} }}\right)^{\frac{\mathrm{1}}{\mathrm{t}}} \\ $$$$=\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\left[\left(\mathrm{1}+\frac{\mathrm{2}−\sqrt{\mathrm{1}+\mathrm{2t}+\mathrm{3t}^{\mathrm{2}} }−\sqrt{\mathrm{1}+\mathrm{3t}^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}+\mathrm{2t}+\mathrm{3t}^{\mathrm{2}} }+\sqrt{\mathrm{1}+\mathrm{3t}^{\mathrm{2}} }}\right)^{\frac{\mathrm{1}}{\Box}} \right]^{\frac{\Box}{\mathrm{t}}} \\ $$$$=\mathrm{e}^{\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}−\sqrt{\mathrm{1}+\mathrm{2t}+\mathrm{3t}^{\mathrm{2}} }−\sqrt{\mathrm{1}+\mathrm{3t}^{\mathrm{2}} }}{\:\left(\sqrt{\mathrm{1}+\mathrm{2t}+\mathrm{3t}^{\mathrm{2}} }+\sqrt{\mathrm{1}+\mathrm{3t}^{\mathrm{2}} }\right)\mathrm{t}}} =\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{1}−\sqrt{\mathrm{1}+\mathrm{2t}+\mathrm{3t}^{\mathrm{2}} }}{\mathrm{t}}+\frac{\mathrm{1}−\sqrt{\mathrm{1}+\mathrm{3t}^{\mathrm{2}} }}{\mathrm{t}}\right)} \\ $$$$=\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{−\mathrm{2}−\mathrm{3t}}{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{2t}+\mathrm{3t}^{\mathrm{2}} }}−\frac{\mathrm{3t}}{\:\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{3t}^{\mathrm{2}} }}\right)} \\ $$$$=\mathrm{e}^{−\frac{\mathrm{1}}{\mathrm{2}}} =\frac{\mathrm{1}}{\:\sqrt{\mathrm{e}}} \\ $$
Answered by floor(10²Eta[1]) last updated on 03/Jul/22
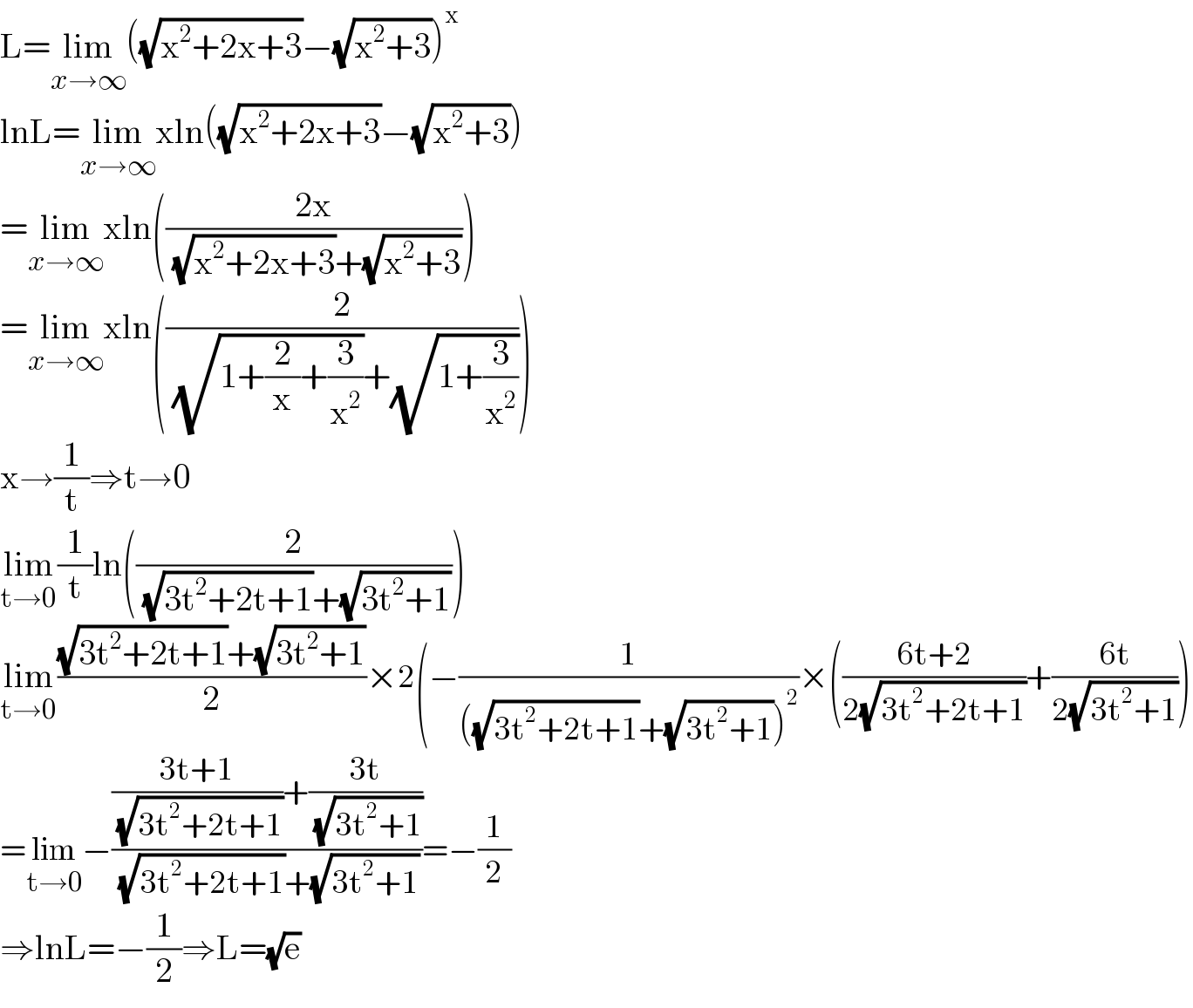
$$\mathrm{L}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{3}}−\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{3}}\right)^{\mathrm{x}} \\ $$$$\mathrm{lnL}=\underset{{x}\rightarrow\infty} {\mathrm{lim}xln}\left(\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{3}}−\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{3}}\right) \\ $$$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}xln}\left(\frac{\mathrm{2x}}{\:\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{2x}+\mathrm{3}}+\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{3}}}\right) \\ $$$$=\underset{{x}\rightarrow\infty} {\mathrm{lim}xln}\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{1}+\frac{\mathrm{2}}{\mathrm{x}}+\frac{\mathrm{3}}{\mathrm{x}^{\mathrm{2}} }}+\sqrt{\mathrm{1}+\frac{\mathrm{3}}{\mathrm{x}^{\mathrm{2}} }}}\right) \\ $$$$\mathrm{x}\rightarrow\frac{\mathrm{1}}{\mathrm{t}}\Rightarrow\mathrm{t}\rightarrow\mathrm{0} \\ $$$$\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{\mathrm{t}}\mathrm{ln}\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{3t}^{\mathrm{2}} +\mathrm{2t}+\mathrm{1}}+\sqrt{\mathrm{3t}^{\mathrm{2}} +\mathrm{1}}}\right) \\ $$$$\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\sqrt{\mathrm{3t}^{\mathrm{2}} +\mathrm{2t}+\mathrm{1}}+\sqrt{\mathrm{3t}^{\mathrm{2}} +\mathrm{1}}}{\mathrm{2}}×\mathrm{2}\left(−\frac{\mathrm{1}}{\left(\sqrt{\mathrm{3t}^{\mathrm{2}} +\mathrm{2t}+\mathrm{1}}+\sqrt{\mathrm{3t}^{\mathrm{2}} +\mathrm{1}}\right)^{\mathrm{2}} }×\left(\frac{\mathrm{6t}+\mathrm{2}}{\mathrm{2}\sqrt{\mathrm{3t}^{\mathrm{2}} +\mathrm{2t}+\mathrm{1}}}+\frac{\mathrm{6t}}{\mathrm{2}\sqrt{\mathrm{3t}^{\mathrm{2}} +\mathrm{1}}}\right)\right. \\ $$$$=\underset{\mathrm{t}\rightarrow\mathrm{0}} {\mathrm{lim}}−\frac{\frac{\mathrm{3t}+\mathrm{1}}{\:\sqrt{\mathrm{3t}^{\mathrm{2}} +\mathrm{2t}+\mathrm{1}}}+\frac{\mathrm{3t}}{\:\sqrt{\mathrm{3t}^{\mathrm{2}} +\mathrm{1}}}}{\:\sqrt{\mathrm{3t}^{\mathrm{2}} +\mathrm{2t}+\mathrm{1}}+\sqrt{\mathrm{3t}^{\mathrm{2}} +\mathrm{1}}}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{lnL}=−\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\mathrm{L}=\sqrt{\mathrm{e}} \\ $$
