Question Number 122671 by mnjuly1970 last updated on 18/Nov/20
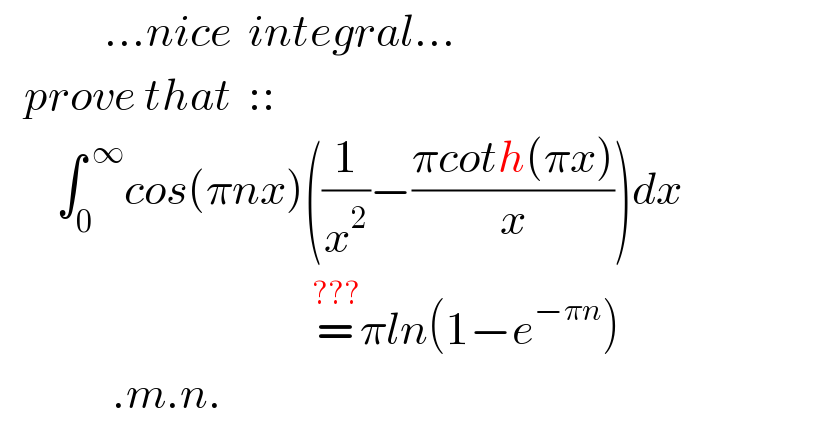
$$\:\:\:\:\:\:\:\:\:\:\:\:\:…{nice}\:\:{integral}… \\ $$$$\:\:\:{prove}\:{that}\:\::: \\ $$$$\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\infty} {cos}\left(\pi{nx}\right)\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\pi{coth}\left(\pi{x}\right)}{{x}}\right){dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\overset{???} {=}\pi{ln}\left(\mathrm{1}−{e}^{−\pi{n}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:.{m}.{n}. \\ $$
Commented by mnjuly1970 last updated on 19/Nov/20

$${grateful}\:{mr}\:{mindspower}. \\ $$$$\:\:''\:{complex}\:{analysis}'. \\ $$$$\:\:{very}\:{nice}\:{solution}\: \\ $$$$\:\:\:\:{residues}\:{theorey}\:{and}\:{singularities}.. \\ $$
Commented by mindispower last updated on 19/Nov/20
$${withe}\:{pleasur}\:{sir}\:{nice}\:{day} \\ $$
Answered by mindispower last updated on 19/Nov/20
![(1/2)∫_(−∞) ^∞ cos(πnx)((1/x^2 )−(π/x)coth(πx))dx=(1/2)∫cos(πnx)f(x)dx pols of f ⇔ e^(πx) =e^(−πx) ⇒e^(2πx) =1⇒x=ik for k=0 removabal singularity Res(f,0)=0 Res(f,ik)=lim_(x→ik) (x−ik).((sh(πx)−πxch(πx))/(x^2 sh(πx))) =((sh(iπk)−πikch(πik))/((ik)^2 .πch(ikπ)))=(i/k),k∈Z^∗ residue over D=C_R ∪[−R,−ε[]ε,R[, C_R =Re^(iθ) ,θ∈[0,π[⇒x∈D,Imx>0, pols are ik,k∈N^∗ ⇔(1/2)Re∫_(−∞) ^∞ e^(iπnx) f(x)dx ∫_(−∞) ^∞ e^(iπnx) f(x)dx=2iπRes(e^(iπnx) f,ik) =2iπΣ_(k≥1) e^(−nπk) .(i/k)=2π(−Σ_(k≥1) (((e^(−nπ) )^k )/k) ) =2πln(1−e^(−nπ) ) ∫_0 ^∞ cos(πnx)((1/x^2 )−π((coth(πx))/x) )dx =(1/2)Re∫_(−∞) ^∞ e^(iπnx) f(x)dx=(1/2).2πln(1−e^(−nπ) ) =πln(1−e^(−nπ) )](https://www.tinkutara.com/question/Q122712.png)
$$\frac{\mathrm{1}}{\mathrm{2}}\int_{−\infty} ^{\infty} {cos}\left(\pi{nx}\right)\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\pi}{{x}}{coth}\left(\pi{x}\right)\right){dx}=\frac{\mathrm{1}}{\mathrm{2}}\int{cos}\left(\pi{nx}\right){f}\left({x}\right){dx} \\ $$$${pols}\:{of}\:{f}\:\Leftrightarrow \\ $$$$ \\ $$$${e}^{\pi{x}} ={e}^{−\pi{x}} \Rightarrow{e}^{\mathrm{2}\pi{x}} =\mathrm{1}\Rightarrow{x}={ik} \\ $$$${for}\:{k}=\mathrm{0}\:\:{removabal}\:{singularity} \\ $$$${Res}\left({f},\mathrm{0}\right)=\mathrm{0} \\ $$$${Res}\left({f},{ik}\right)=\underset{{x}\rightarrow{ik}} {\mathrm{lim}}\left({x}−{ik}\right).\frac{{sh}\left(\pi{x}\right)−\pi{xch}\left(\pi{x}\right)}{{x}^{\mathrm{2}} {sh}\left(\pi{x}\right)} \\ $$$$=\frac{{sh}\left({i}\pi{k}\right)−\pi{ikch}\left(\pi{ik}\right)}{\left({ik}\right)^{\mathrm{2}} .\pi{ch}\left({ik}\pi\right)}=\frac{{i}}{{k}},{k}\in\mathbb{Z}^{\ast} \\ $$$${residue}\:{over}\:{D}={C}_{{R}} \cup\left[−{R},−\epsilon\left[\right]\epsilon,{R}\left[,\right.\right. \\ $$$${C}_{{R}} ={Re}^{{i}\theta} ,\theta\in\left[\mathrm{0},\pi\left[\Rightarrow{x}\in{D},{Imx}>\mathrm{0},\:{pols}\:{are}\:{ik},{k}\in\mathbb{N}^{\ast} \right.\right. \\ $$$$\Leftrightarrow\frac{\mathrm{1}}{\mathrm{2}}{Re}\int_{−\infty} ^{\infty} {e}^{{i}\pi{nx}} {f}\left({x}\right){dx} \\ $$$$\int_{−\infty} ^{\infty} {e}^{{i}\pi{nx}} {f}\left({x}\right){dx}=\mathrm{2}{i}\pi{Res}\left({e}^{{i}\pi{nx}} {f},{ik}\right) \\ $$$$=\mathrm{2}{i}\pi\underset{{k}\geqslant\mathrm{1}} {\sum}{e}^{−{n}\pi{k}} .\frac{{i}}{{k}}=\mathrm{2}\pi\left(−\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left({e}^{−{n}\pi} \right)^{{k}} }{{k}}\:\right) \\ $$$$=\mathrm{2}\pi{ln}\left(\mathrm{1}−{e}^{−{n}\pi} \right) \\ $$$$\int_{\mathrm{0}} ^{\infty} {cos}\left(\pi{nx}\right)\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\pi\frac{{coth}\left(\pi{x}\right)}{{x}}\:\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{Re}\int_{−\infty} ^{\infty} {e}^{{i}\pi{nx}} {f}\left({x}\right){dx}=\frac{\mathrm{1}}{\mathrm{2}}.\mathrm{2}\pi{ln}\left(\mathrm{1}−{e}^{−{n}\pi} \right) \\ $$$$=\pi{ln}\left(\mathrm{1}−{e}^{−{n}\pi} \right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 19/Nov/20
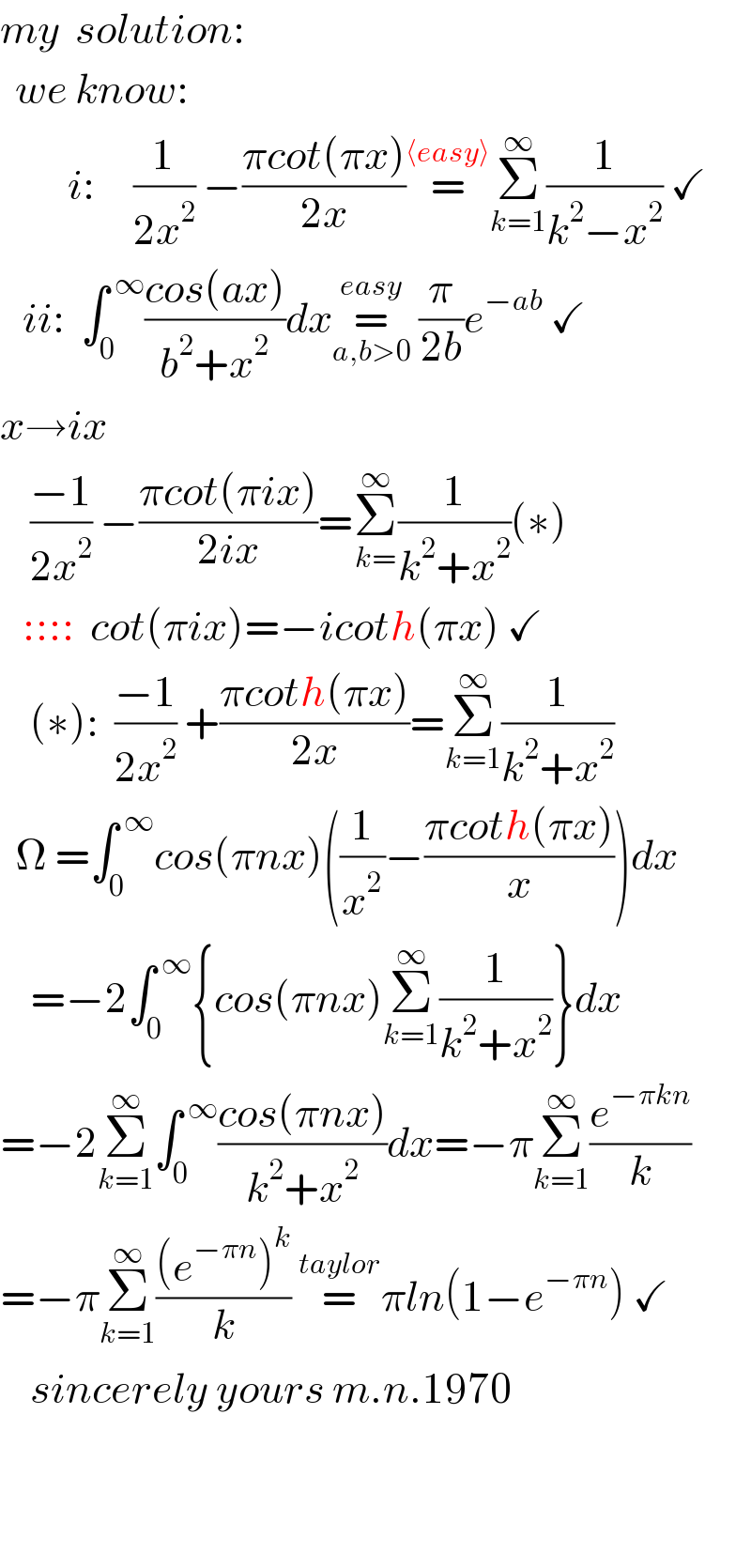
$${my}\:\:{solution}: \\ $$$$\:\:{we}\:{know}: \\ $$$$\:\:\:\:\:\:\:\:\:{i}:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }\:−\frac{\pi{cot}\left(\pi{x}\right)}{\mathrm{2}{x}}\overset{\langle{easy}\rangle} {=}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{2}} −{x}^{\mathrm{2}} }\:\checkmark \\ $$$$\:\:\:{ii}:\:\:\int_{\mathrm{0}} ^{\:\infty} \frac{{cos}\left({ax}\right)}{{b}^{\mathrm{2}} +{x}^{\mathrm{2}} }{dx}\underset{{a},{b}>\mathrm{0}} {\overset{{easy}} {=}}\:\frac{\pi}{\mathrm{2}{b}}{e}^{−{ab}} \:\checkmark \\ $$$${x}\rightarrow{ix} \\ $$$$\:\:\:\:\frac{−\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }\:−\frac{\pi{cot}\left(\pi{ix}\right)}{\mathrm{2}{ix}}=\underset{{k}=} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{2}} +{x}^{\mathrm{2}} }\left(\ast\right) \\ $$$$\:\:\:::::\:\:{cot}\left(\pi{ix}\right)=−{icoth}\left(\pi{x}\right)\:\checkmark \\ $$$$\:\:\:\:\left(\ast\right):\:\:\frac{−\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }\:+\frac{\pi{coth}\left(\pi{x}\right)}{\mathrm{2}{x}}=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{2}} +{x}^{\mathrm{2}} } \\ $$$$\:\:\Omega\:=\int_{\mathrm{0}} ^{\:\infty} {cos}\left(\pi{nx}\right)\left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }−\frac{\pi{coth}\left(\pi{x}\right)}{{x}}\right){dx} \\ $$$$\:\:\:\:=−\mathrm{2}\int_{\mathrm{0}} ^{\:\infty} \left\{{cos}\left(\pi{nx}\right)\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{2}} +{x}^{\mathrm{2}} }\right\}{dx} \\ $$$$=−\mathrm{2}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\:\infty} \frac{{cos}\left(\pi{nx}\right)}{{k}^{\mathrm{2}} +{x}^{\mathrm{2}} }{dx}=−\pi\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{e}^{−\pi{kn}} }{{k}} \\ $$$$=−\pi\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left({e}^{−\pi{n}} \right)^{{k}} }{{k}}\:\overset{{taylor}} {=}\pi{ln}\left(\mathrm{1}−{e}^{−\pi{n}} \right)\:\checkmark \\ $$$$\:\:\:\:{sincerely}\:{yours}\:{m}.{n}.\mathrm{1970} \\ $$$$ \\ $$$$ \\ $$
