Question Number 109097 by bobhans last updated on 21/Aug/20
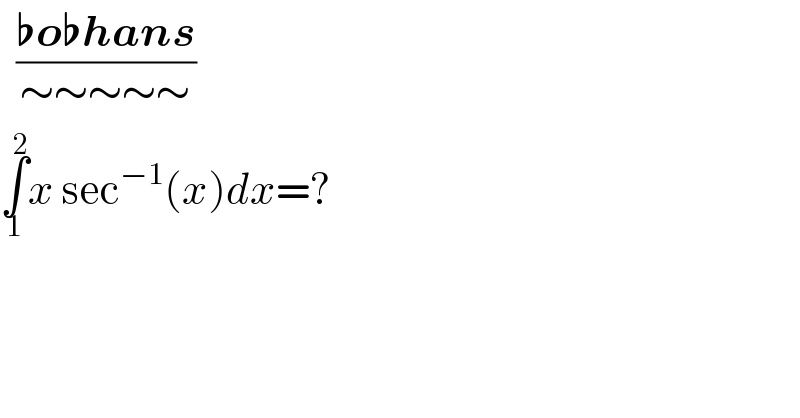
$$\:\:\frac{\boldsymbol{\flat{o}\flat{hans}}}{\sim\sim\sim\sim\sim} \\ $$$$\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}{x}\:\mathrm{sec}^{−\mathrm{1}} \left({x}\right){dx}=? \\ $$
Answered by john santu last updated on 21/Aug/20
![((⊸JS⊸)/(∤…∤…∤)) I=∫_1 ^2 x sec^(−1) (x) dx → { ((sec^(−1) (x)=k, x=sec k)),((x=1,k=0, x=2,k=(π/3))) :} I=∫_0 ^(π/3) k. sec k (sec k.tan k dk ) I=∫_0 ^(π/3) k.sec^2 k.tan k dk [ by parts → { ((u=k)),((v=∫tan k d(tan k)=(1/2)tan^2 k)) :}] I=(1/2)k.tan^2 k ]_0 ^(π/3) −(1/2)∫tan^2 k dk I=(1/2).(π/3).((√3))^2 −(1/2)∫ (sec^2 k−1)dk I=(π/2)−(1/2)[tan k−k ]_0 ^(π/3) I=(π/2)−(1/2)[((√3)−(π/3))−(0)] I=(π/2)−((√3)/2)+(π/6) = ((2π)/3)−((√3)/2).](https://www.tinkutara.com/question/Q109098.png)
$$\:\:\:\:\frac{\multimap{JS}\multimap}{\nmid\ldots\nmid\ldots\nmid} \\ $$$${I}=\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}{x}\:\mathrm{sec}^{−\mathrm{1}} \left({x}\right)\:{dx}\:\rightarrow\begin{cases}{\mathrm{sec}^{−\mathrm{1}} \left({x}\right)={k},\:{x}=\mathrm{sec}\:{k}}\\{{x}=\mathrm{1},{k}=\mathrm{0},\:{x}=\mathrm{2},{k}=\frac{\pi}{\mathrm{3}}}\end{cases} \\ $$$${I}=\underset{\mathrm{0}} {\overset{\pi/\mathrm{3}} {\int}}{k}.\:\mathrm{sec}\:{k}\:\left(\mathrm{sec}\:{k}.\mathrm{tan}\:{k}\:{dk}\:\right) \\ $$$${I}=\underset{\mathrm{0}} {\overset{\pi/\mathrm{3}} {\int}}{k}.\mathrm{sec}\:^{\mathrm{2}} {k}.\mathrm{tan}\:{k}\:{dk}\: \\ $$$$\left[\:{by}\:{parts}\:\rightarrow\begin{cases}{{u}={k}}\\{{v}=\int\mathrm{tan}\:{k}\:{d}\left(\mathrm{tan}\:{k}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}\:^{\mathrm{2}} {k}}\end{cases}\right] \\ $$$$\left.{I}=\frac{\mathrm{1}}{\mathrm{2}}{k}.\mathrm{tan}\:^{\mathrm{2}} {k}\:\right]_{\mathrm{0}} ^{\pi/\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{tan}\:^{\mathrm{2}} {k}\:{dk}\: \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\pi}{\mathrm{3}}.\left(\sqrt{\mathrm{3}}\right)^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2}}\int\:\left(\mathrm{sec}\:^{\mathrm{2}} {k}−\mathrm{1}\right){dk} \\ $$$${I}=\frac{\pi}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\left[\mathrm{tan}\:{k}−{k}\:\right]_{\mathrm{0}} ^{\pi/\mathrm{3}} \\ $$$${I}=\frac{\pi}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\left[\left(\sqrt{\mathrm{3}}−\frac{\pi}{\mathrm{3}}\right)−\left(\mathrm{0}\right)\right] \\ $$$${I}=\frac{\pi}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\frac{\pi}{\mathrm{6}}\:=\:\frac{\mathrm{2}\pi}{\mathrm{3}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}.\: \\ $$$$ \\ $$
