Question Number 99623 by hardylanes last updated on 22/Jun/20

$${obtain}\:{the}\:{modulus}\:{and}\:{arguement}\:{of} \\ $$$$\frac{\left(\mathrm{1}−{i}\right)^{\mathrm{4}} }{\left(\mathrm{2}+\mathrm{2}\sqrt{\left.\mathrm{3}{i}\right)^{\mathrm{3}} }\right.} \\ $$
Commented by Dwaipayan Shikari last updated on 22/Jun/20
![=(((1−i)^(2.2) )/(4^3 ((1/2)+((√3)/2)i)^3 ))=(((−2i)^2 )/(64e^(((πi)/3).3) ))=((−4)/(64 e^(πi) ))=((−4)/(−64))=(1/(16))+0.i=z mod (z) is (1/(16)) arg(z) is 0 [As α=tan^(−1) ((0/(1/(16))))=0 ]{And e^(πi) =−1}](https://www.tinkutara.com/question/Q99635.png)
$$=\frac{\left(\mathrm{1}−{i}\right)^{\mathrm{2}.\mathrm{2}} }{\mathrm{4}^{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i}\right)^{\mathrm{3}} }=\frac{\left(−\mathrm{2}{i}\right)^{\mathrm{2}} }{\mathrm{64}{e}^{\frac{\pi{i}}{\mathrm{3}}.\mathrm{3}} }=\frac{−\mathrm{4}}{\mathrm{64}\:{e}^{\pi{i}} }=\frac{−\mathrm{4}}{−\mathrm{64}}=\frac{\mathrm{1}}{\mathrm{16}}+\mathrm{0}.{i}={z} \\ $$$${mod}\:\left({z}\right)\:{is}\:\frac{\mathrm{1}}{\mathrm{16}} \\ $$$${arg}\left({z}\right)\:{is}\:\mathrm{0}\:\:\:\left[{As}\:\alpha=\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{0}}{\frac{\mathrm{1}}{\mathrm{16}}}\right)=\mathrm{0}\:\:\right]\left\{{And}\:\:{e}^{\pi{i}} =−\mathrm{1}\right\} \\ $$
Answered by Rio Michael last updated on 22/Jun/20
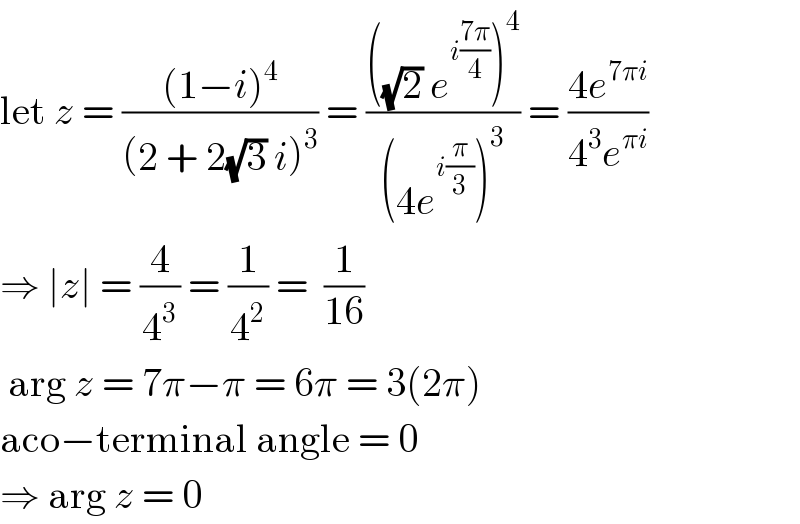
$$\mathrm{let}\:{z}\:=\:\frac{\left(\mathrm{1}−{i}\right)^{\mathrm{4}} }{\left(\mathrm{2}\:+\:\mathrm{2}\sqrt{\mathrm{3}}\:{i}\right)^{\mathrm{3}} }\:=\:\frac{\left(\sqrt{\mathrm{2}}\:{e}^{{i}\frac{\mathrm{7}\pi}{\mathrm{4}}} \right)^{\mathrm{4}} }{\left(\mathrm{4}{e}^{{i}\frac{\pi}{\mathrm{3}}} \right)^{\mathrm{3}} }\:=\:\frac{\mathrm{4}{e}^{\mathrm{7}\pi{i}} }{\mathrm{4}^{\mathrm{3}} {e}^{\pi{i}} } \\ $$$$\Rightarrow\:\mid{z}\mid\:=\:\frac{\mathrm{4}}{\mathrm{4}^{\mathrm{3}} }\:=\:\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{2}} }\:=\:\:\frac{\mathrm{1}}{\mathrm{16}} \\ $$$$\:\mathrm{arg}\:{z}\:=\:\mathrm{7}\pi−\pi\:=\:\mathrm{6}\pi\:=\:\mathrm{3}\left(\mathrm{2}\pi\right) \\ $$$$\mathrm{aco}−\mathrm{terminal}\:\mathrm{angle}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{arg}\:{z}\:=\:\mathrm{0} \\ $$
Commented by mathmax by abdo last updated on 23/Jun/20
![z =(((1−i)^4 )/((2+2(√3)i)^3 )) we have 1−i =(√2)e^(−((iπ)/4)) ⇒(1−i)^4 =4 e^(−iπ) 2+2(√3)i =2(1+(√3)i) =4((1/2)+((i(√3))/2)) =4e^((iπ)/3) ⇒(2+2(√3)i)^3 =4^3 e^((4iπ)/3) ⇒ z =(1/(16)) e^(−iπ−((4iπ)/3)) =(1/(16)) e^(−i(π+((4π)/3))) =(1/(16)) e^(−i(((7π)/3))) =(1/(16)) e^(−i(2π +(π/3))) =(1/(16)) e^(−((iπ)/3)) ⇒ ∣z∣ =(1/(16)) and argz ≡−(π/3)[2π]](https://www.tinkutara.com/question/Q99787.png)
$$\mathrm{z}\:=\frac{\left(\mathrm{1}−\mathrm{i}\right)^{\mathrm{4}} }{\left(\mathrm{2}+\mathrm{2}\sqrt{\mathrm{3}}\mathrm{i}\right)^{\mathrm{3}} }\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{1}−\mathrm{i}\:=\sqrt{\mathrm{2}}\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{4}}} \:\Rightarrow\left(\mathrm{1}−\mathrm{i}\right)^{\mathrm{4}} \:=\mathrm{4}\:\mathrm{e}^{−\mathrm{i}\pi} \: \\ $$$$\mathrm{2}+\mathrm{2}\sqrt{\mathrm{3}}\mathrm{i}\:=\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{3}}\mathrm{i}\right)\:=\mathrm{4}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{i}\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\:=\mathrm{4e}^{\frac{\mathrm{i}\pi}{\mathrm{3}}} \:\Rightarrow\left(\mathrm{2}+\mathrm{2}\sqrt{\mathrm{3}}\mathrm{i}\right)^{\mathrm{3}} \:=\mathrm{4}^{\mathrm{3}} \:\mathrm{e}^{\frac{\mathrm{4i}\pi}{\mathrm{3}}} \:\Rightarrow \\ $$$$\mathrm{z}\:=\frac{\mathrm{1}}{\mathrm{16}}\:\mathrm{e}^{−\mathrm{i}\pi−\frac{\mathrm{4i}\pi}{\mathrm{3}}} \:=\frac{\mathrm{1}}{\mathrm{16}}\:\mathrm{e}^{−\mathrm{i}\left(\pi+\frac{\mathrm{4}\pi}{\mathrm{3}}\right)} \:=\frac{\mathrm{1}}{\mathrm{16}}\:\mathrm{e}^{−\mathrm{i}\left(\frac{\mathrm{7}\pi}{\mathrm{3}}\right)} \:=\frac{\mathrm{1}}{\mathrm{16}}\:\mathrm{e}^{−\mathrm{i}\left(\mathrm{2}\pi\:+\frac{\pi}{\mathrm{3}}\right)} \:=\frac{\mathrm{1}}{\mathrm{16}}\:\mathrm{e}^{−\frac{\mathrm{i}\pi}{\mathrm{3}}} \:\Rightarrow \\ $$$$\mid\mathrm{z}\mid\:=\frac{\mathrm{1}}{\mathrm{16}}\:\mathrm{and}\:\mathrm{argz}\:\equiv−\frac{\pi}{\mathrm{3}}\left[\mathrm{2}\pi\right] \\ $$
