Question Number 118340 by bramlexs22 last updated on 17/Oct/20
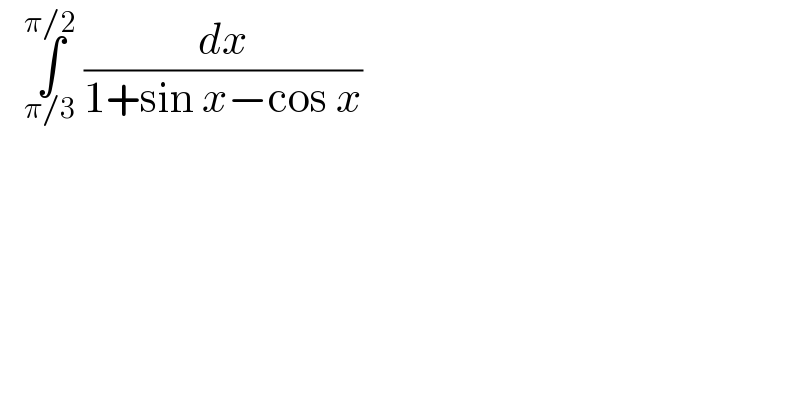
$$\:\:\:\underset{\pi/\mathrm{3}} {\overset{\pi/\mathrm{2}} {\int}}\:\frac{{dx}}{\mathrm{1}+\mathrm{sin}\:{x}−\mathrm{cos}\:{x}} \\ $$
Commented by Dwaipayan Shikari last updated on 17/Oct/20
![∫_(π/3) ^(π/2) (dx/(1−cosx+sinx))=2∫_(1/( (√3))) ^1 (dt/(1−((1−t^2 )/(1+t^2 ))+((2t)/(1+t^2 )))).(1/(1+t^2 )) x=tan(x/2) =2∫_(1/( (√3))) ^1 (dt/(2t^2 +2t))=∫_(1/( (√3))) ^1 (dt/(t(t+1)))=[log((t/(t+1)))]_(1/( (√3))) ^1 =log((1/2))−log((1/( (√3)+1)))=log((((√3)+1)/2))](https://www.tinkutara.com/question/Q118353.png)
$$\int_{\frac{\pi}{\mathrm{3}}} ^{\frac{\pi}{\mathrm{2}}} \frac{{dx}}{\mathrm{1}−{cosx}+{sinx}}=\mathrm{2}\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\mathrm{1}} \frac{{dt}}{\mathrm{1}−\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }}.\frac{\mathrm{1}}{\mathrm{1}+{t}^{\mathrm{2}} }\:\:\:\:\:\:\:{x}={tan}\frac{{x}}{\mathrm{2}} \\ $$$$=\mathrm{2}\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\mathrm{1}} \frac{{dt}}{\mathrm{2}{t}^{\mathrm{2}} +\mathrm{2}{t}}=\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\mathrm{1}} \frac{{dt}}{{t}\left({t}+\mathrm{1}\right)}=\left[{log}\left(\frac{{t}}{{t}+\mathrm{1}}\right)\right]_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\mathrm{1}} \\ $$$$={log}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−{log}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}+\mathrm{1}}\right)={log}\left(\frac{\sqrt{\mathrm{3}}+\mathrm{1}}{\mathrm{2}}\right) \\ $$$$ \\ $$
Answered by Bird last updated on 17/Oct/20
![I =∫_(π/3) ^(π/2) (dx/(1+sinx−cosx)) we do the ch.tan((x/2))=t ⇒ I =∫_(1/( (√3))) ^1 ((2dt)/((1+t^2 )(1+((2t)/(1+t^2 ))−((1−t^2 )/(1+t^2 ))))) =∫_(1/( (√3))) ^1 ((2dt)/(1+t^2 +2t−1+t^2 )) =∫_(1/( (√3))) ^1 ((2dt)/(2t^2 +2t)) =∫_(1/( (√3))) ^1 (dt/(t(t+1))) =∫_(1/( (√3))) ^1 ((1/t)−(1/(t+1)))dt =[ln∣(t/(t+1))∣]_(1/( (√3))) ^1 =ln((1/2))−ln((1/( (√3)(1+(1/( (√3))))))) =−ln(2)+ln(1+(√3))](https://www.tinkutara.com/question/Q118416.png)
$${I}\:=\int_{\frac{\pi}{\mathrm{3}}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{dx}}{\mathrm{1}+{sinx}−{cosx}} \\ $$$${we}\:{do}\:{the}\:{ch}.{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:\Rightarrow \\ $$$${I}\:=\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\mathrm{1}} \:\:\:\frac{\mathrm{2}{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{1}+\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }−\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }\right)} \\ $$$$=\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}{dt}}{\mathrm{2}{t}^{\mathrm{2}} +\mathrm{2}{t}}\:=\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\mathrm{1}} \:\frac{{dt}}{{t}\left({t}+\mathrm{1}\right)} \\ $$$$=\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\mathrm{1}} \:\left(\frac{\mathrm{1}}{{t}}−\frac{\mathrm{1}}{{t}+\mathrm{1}}\right){dt} \\ $$$$=\left[{ln}\mid\frac{{t}}{{t}+\mathrm{1}}\mid\right]_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\mathrm{1}} ={ln}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−{ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}\left(\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)}\right) \\ $$$$=−{ln}\left(\mathrm{2}\right)+{ln}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right) \\ $$$$ \\ $$
