Question Number 21707 by Isse last updated on 01/Oct/17
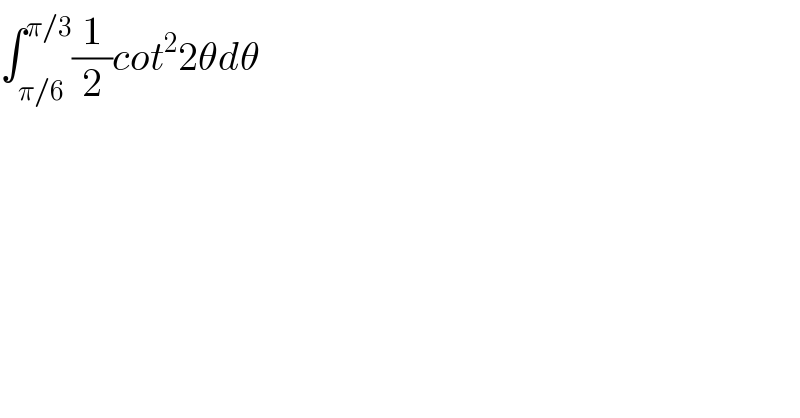
$$\int_{\pi/\mathrm{6}} ^{\pi/\mathrm{3}} \frac{\mathrm{1}}{\mathrm{2}}{cot}^{\mathrm{2}} \mathrm{2}\theta{d}\theta \\ $$
Commented by Tikufly last updated on 01/Oct/17
![I=(1/2)∫_(π/6) ^(π/3) (cosec^2 2θ−1)dθ =(1/2)∫_(π/6) ^(π/3) cosec^2 2θ−(1/2)∫_(π/6) ^(π/3) 1dθ =−(1/4)[cot2θ]_(π/6) ^(π/3) −(1/2)[θ]_(π/6) ^(π/3) =−(1/4){cot(((2θ)/3))−cot((θ/3))}−(1/2)((π/3)−(π/6)) =−(1/4)(−(1/( (√3)))−(1/( (√3))))−(1/2)((π/6)) =(1/(2(√3)))−(π/(12))](https://www.tinkutara.com/question/Q21712.png)
$$\mathrm{I}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\pi/\mathrm{6}} ^{\pi/\mathrm{3}} \left(\mathrm{cosec}^{\mathrm{2}} \mathrm{2}\theta−\mathrm{1}\right)\mathrm{d}\theta \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\pi/\mathrm{6}} ^{\pi/\mathrm{3}} \mathrm{cosec}^{\mathrm{2}} \mathrm{2}\theta−\frac{\mathrm{1}}{\mathrm{2}}\int_{\pi/\mathrm{6}} ^{\pi/\mathrm{3}} \mathrm{1d}\theta \\ $$$$\:\:=−\frac{\mathrm{1}}{\mathrm{4}}\left[\mathrm{cot2}\theta\right]_{\pi/\mathrm{6}} ^{\pi/\mathrm{3}} \:−\frac{\mathrm{1}}{\mathrm{2}}\left[\theta\right]_{\pi/\mathrm{6}} ^{\pi/\mathrm{3}} \\ $$$$\:\:=−\frac{\mathrm{1}}{\mathrm{4}}\left\{\mathrm{cot}\left(\frac{\mathrm{2}\theta}{\mathrm{3}}\right)−\mathrm{cot}\left(\frac{\theta}{\mathrm{3}}\right)\right\}−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{3}}−\frac{\pi}{\mathrm{6}}\right) \\ $$$$\:\:=−\frac{\mathrm{1}}{\mathrm{4}}\left(−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)−\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi}{\mathrm{6}}\right) \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}−\frac{\pi}{\mathrm{12}} \\ $$
Commented by Isse last updated on 01/Oct/17

$${thanks} \\ $$
Commented by Tikufly last updated on 02/Oct/17

$$\mathrm{Welcome} \\ $$
