please-help-integrate-x-sin-x-1-cos-x-dx-

Question Number 50633 by Necxx last updated on 18/Dec/18

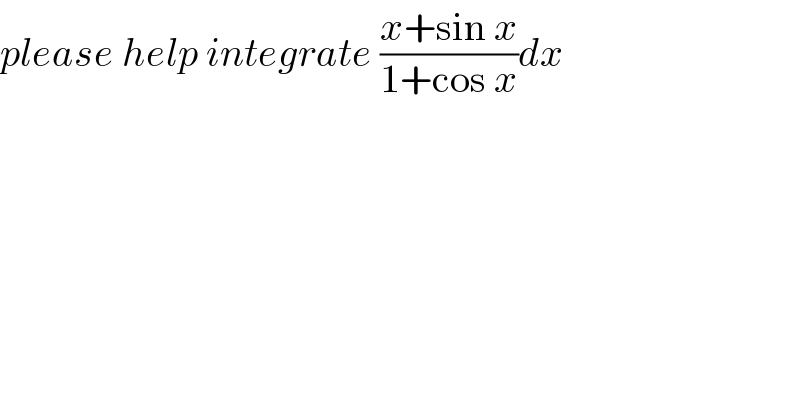
$${please}\:{help}\:{integrate}\:\frac{{x}+\mathrm{sin}\:{x}}{\mathrm{1}+\mathrm{cos}\:{x}}{dx} \\ $$

Commented by maxmathsup by imad last updated on 18/Dec/18

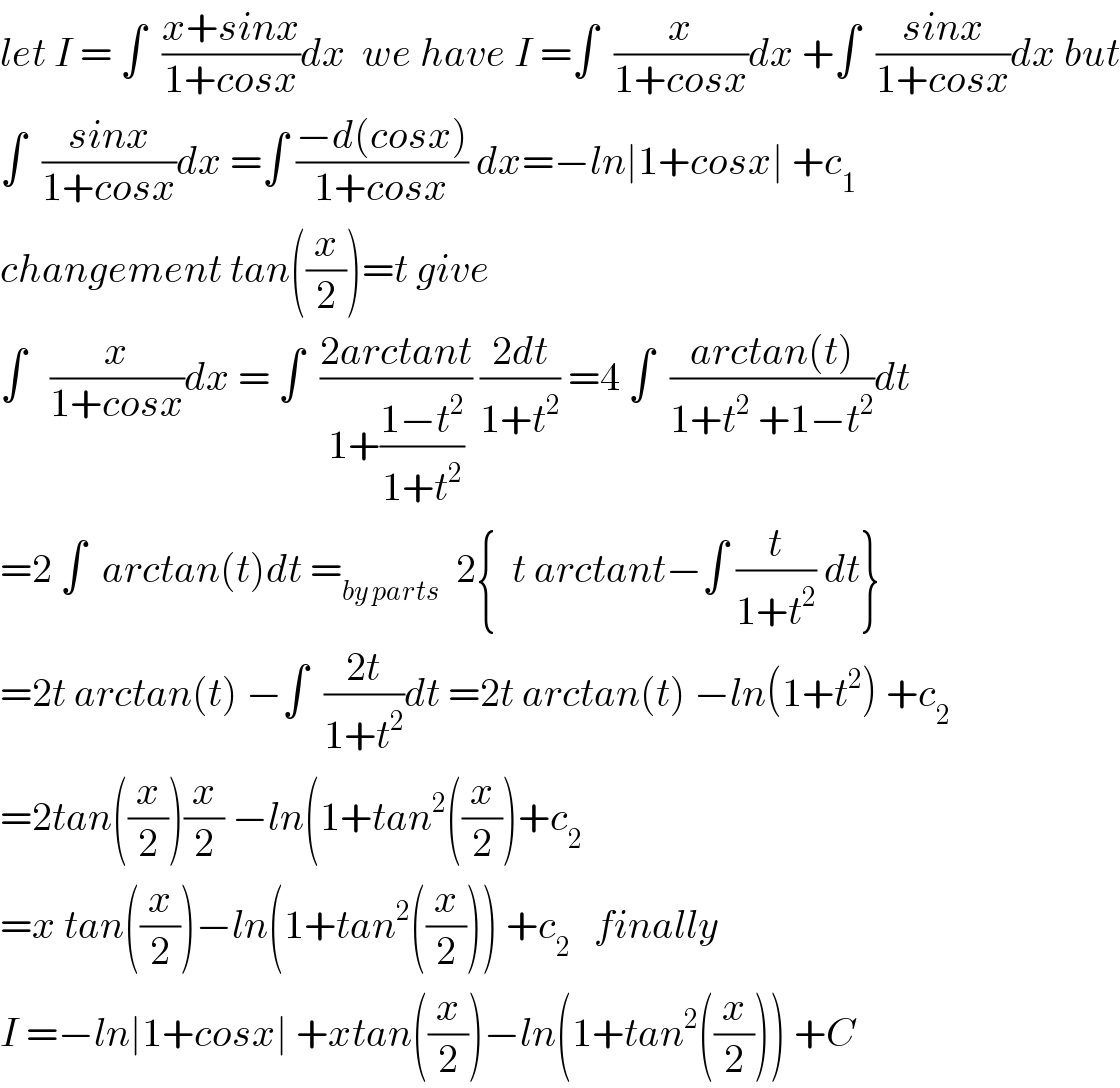
let I = ∫ ((x+sinx)/(1+cosx))dx we have I =∫ (x/(1+cosx))dx +∫ ((sinx)/(1+cosx))dx but ∫ ((sinx)/(1+cosx))dx =∫ ((−d(cosx))/(1+cosx)) dx=−ln∣1+cosx∣ +c_1 changement tan((x/2))=t give ∫ (x/(1+cosx))dx = ∫ ((2arctant)/(1+((1−t^2 )/(1+t^2 )))) ((2dt)/(1+t^2 )) =4 ∫ ((arctan(t))/(1+t^2 +1−t^2 ))dt =2 ∫ arctan(t)dt =_(by parts) 2{ t arctant−∫ (t/(1+t^2 )) dt} =2t arctan(t) −∫ ((2t)/(1+t^2 ))dt =2t arctan(t) −ln(1+t^2 ) +c_2 =2tan((x/2))(x/2) −ln(1+tan^2 ((x/2))+c_2 =x tan((x/2))−ln(1+tan^2 ((x/2))) +c_2 finally I =−ln∣1+cosx∣ +xtan((x/2))−ln(1+tan^2 ((x/2))) +C

$${let}\:{I}\:=\:\int\:\:\frac{{x}+{sinx}}{\mathrm{1}+{cosx}}{dx}\:\:{we}\:{have}\:{I}\:=\int\:\:\frac{{x}}{\mathrm{1}+{cosx}}{dx}\:+\int\:\:\frac{{sinx}}{\mathrm{1}+{cosx}}{dx}\:{but} \\ $$$$\int\:\:\frac{{sinx}}{\mathrm{1}+{cosx}}{dx}\:=\int\:\frac{−{d}\left({cosx}\right)}{\mathrm{1}+{cosx}}\:{dx}=−{ln}\mid\mathrm{1}+{cosx}\mid\:+{c}_{\mathrm{1}} \\ $$$${changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:{give} \\ $$$$\int\:\:\:\frac{{x}}{\mathrm{1}+{cosx}}{dx}\:=\:\int\:\:\frac{\mathrm{2}{arctant}}{\mathrm{1}+\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\mathrm{4}\:\int\:\:\frac{{arctan}\left({t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} \:+\mathrm{1}−{t}^{\mathrm{2}} }{dt} \\ $$$$=\mathrm{2}\:\int\:\:{arctan}\left({t}\right){dt}\:=_{{by}\:{parts}} \:\:\mathrm{2}\left\{\:\:{t}\:{arctant}−\int\:\frac{{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt}\right\} \\ $$$$=\mathrm{2}{t}\:{arctan}\left({t}\right)\:−\int\:\:\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }{dt}\:=\mathrm{2}{t}\:{arctan}\left({t}\right)\:−{ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\:+{c}_{\mathrm{2}} \\ $$$$=\mathrm{2}{tan}\left(\frac{{x}}{\mathrm{2}}\right)\frac{{x}}{\mathrm{2}}\:−{ln}\left(\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)+{c}_{\mathrm{2}} \right. \\ $$$$={x}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)−{ln}\left(\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right)\:+{c}_{\mathrm{2}} \:\:\:{finally} \\ $$$${I}\:=−{ln}\mid\mathrm{1}+{cosx}\mid\:+{xtan}\left(\frac{{x}}{\mathrm{2}}\right)−{ln}\left(\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right)\:+{C} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 18/Dec/18

∫((x+2sin((x/2))cos((x/2)))/(2cos^2 ((x/2))))dx ∫[((xsec^2 ((x/2)))/2)+tan((x/2))]dx ∫[x.(d/dx)(tan(x/2))+tan((x/2))(dx/dx)]dx ∫(d/dx)(xtan(x/2))dx ∫d(xtan(x/2)) xtan(x/2)+c

$$\int\frac{{x}+\mathrm{2}{sin}\left(\frac{{x}}{\mathrm{2}}\right){cos}\left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{2}{cos}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{dx} \\ $$$$\int\left[\frac{{xsec}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)}{\mathrm{2}}+{tan}\left(\frac{{x}}{\mathrm{2}}\right)\right]{dx} \\ $$$$\int\left[{x}.\frac{{d}}{{dx}}\left({tan}\frac{{x}}{\mathrm{2}}\right)+{tan}\left(\frac{{x}}{\mathrm{2}}\right)\frac{{dx}}{{dx}}\right]{dx} \\ $$$$\int\frac{{d}}{{dx}}\left({xtan}\frac{{x}}{\mathrm{2}}\right){dx} \\ $$$$\int{d}\left({xtan}\frac{{x}}{\mathrm{2}}\right) \\ $$$${xtan}\frac{{x}}{\mathrm{2}}+{c} \\ $$

Commented by ajfour last updated on 18/Dec/18