Question Number 36218 by Rio Mike last updated on 30/May/18
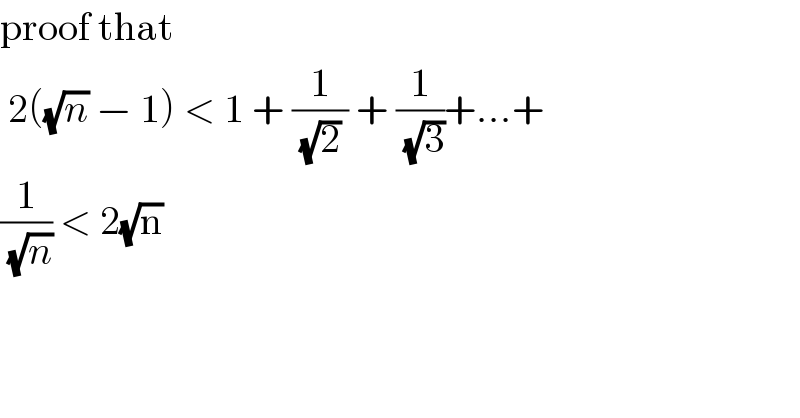
$$\mathrm{proof}\:\mathrm{that}\: \\ $$$$\:\mathrm{2}\left(\sqrt{{n}}\:−\:\mathrm{1}\right)\:<\:\mathrm{1}\:+\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:}\:+\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}+…+ \\ $$$$\frac{\mathrm{1}}{\:\sqrt{{n}}}\:<\:\mathrm{2}\sqrt{\mathrm{n}} \\ $$
Commented by abdo mathsup 649 cc last updated on 30/May/18
![the function f(x)= (1/( (√x))) is decreasing on ]0,+∞[so ∫_k ^(k+1) f(t)dt≤ f(k) ≤ ∫_(k−1) ^k f(t)dt ⇒ Σ_(k=1) ^n ∫_k ^(k+1) f(t)dt ≤ Σ_(k=1) ^n f(k) ≤ Σ_(k=1) ^n ∫_(n−1) ^n f(t)dt ⇒ ∫_1 ^(n+1) (dt/( (√t))) ≤ 1 +(1/( (√2))) +...+(1/( (√n)))≤ ∫_0 ^n (dt/( (√t))) ⇒ [2(√t)]_1 ^(n+1) ≤ 1 +(1/( (√2))) +....+(1/( (√n)))−≤ [2.(√n)]_0 ^n ⇒ 2{(√(n+1)) −1 }≤ 1 +(1/2) +...+(1/( (√n))) ≤ 2(√n) but (√n_ ) ≤.(√(n+1)) ⇒ 2{(√n)−1} ≤ 1+(1/2) +....+(1/( (√n))) ≤ 2(√n) .](https://www.tinkutara.com/question/Q36247.png)
$$\left.{the}\:{function}\:{f}\left({x}\right)=\:\frac{\mathrm{1}}{\:\sqrt{{x}}}\:{is}\:{decreasing}\:{on}\:\right]\mathrm{0},+\infty\left[{so}\right. \\ $$$$\int_{{k}} ^{{k}+\mathrm{1}} {f}\left({t}\right){dt}\leqslant\:{f}\left({k}\right)\:\leqslant\:\int_{{k}−\mathrm{1}} ^{{k}} {f}\left({t}\right){dt}\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \int_{{k}} ^{{k}+\mathrm{1}} {f}\left({t}\right){dt}\:\leqslant\:\sum_{{k}=\mathrm{1}} ^{{n}} {f}\left({k}\right)\:\leqslant\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\int_{{n}−\mathrm{1}} ^{{n}} \:{f}\left({t}\right){dt}\:\Rightarrow \\ $$$$\:\int_{\mathrm{1}} ^{{n}+\mathrm{1}} \frac{{dt}}{\:\sqrt{{t}}}\:\leqslant\:\mathrm{1}\:+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:+…+\frac{\mathrm{1}}{\:\sqrt{{n}}}\leqslant\:\:\int_{\mathrm{0}} ^{{n}} \:\frac{{dt}}{\:\sqrt{{t}}}\:\Rightarrow \\ $$$$\left[\mathrm{2}\sqrt{{t}}\right]_{\mathrm{1}} ^{{n}+\mathrm{1}} \:\leqslant\:\mathrm{1}\:+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:+….+\frac{\mathrm{1}}{\:\sqrt{{n}}}−\leqslant\:\left[\mathrm{2}.\sqrt{{n}}\right]_{\mathrm{0}} ^{{n}} \:\Rightarrow \\ $$$$\mathrm{2}\left\{\sqrt{{n}+\mathrm{1}}\:−\mathrm{1}\:\right\}\leqslant\:\mathrm{1}\:+\frac{\mathrm{1}}{\mathrm{2}}\:+…+\frac{\mathrm{1}}{\:\sqrt{{n}}}\:\leqslant\:\mathrm{2}\sqrt{{n}}\:{but} \\ $$$$\sqrt{{n}_{\:} }\:\:\leqslant.\sqrt{{n}+\mathrm{1}}\:\:\Rightarrow \\ $$$$\mathrm{2}\left\{\sqrt{{n}}−\mathrm{1}\right\}\:\leqslant\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\:+….+\frac{\mathrm{1}}{\:\sqrt{{n}}}\:\leqslant\:\mathrm{2}\sqrt{{n}}\:. \\ $$
