Question Number 63247 by Joel122 last updated on 01/Jul/19
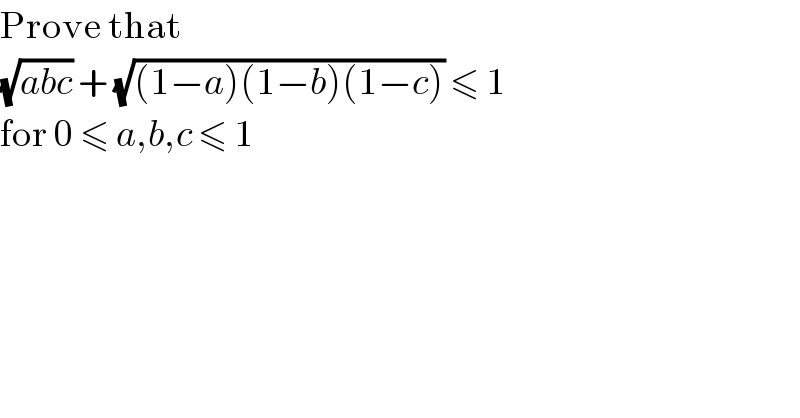
$$\mathrm{Prove}\:\mathrm{that} \\ $$$$\sqrt{{abc}}\:+\:\sqrt{\left(\mathrm{1}−{a}\right)\left(\mathrm{1}−{b}\right)\left(\mathrm{1}−{c}\right)}\:\leqslant\:\mathrm{1} \\ $$$$\mathrm{for}\:\mathrm{0}\:\leqslant\:{a},{b},{c}\:\leqslant\:\mathrm{1} \\ $$
Commented by Tony Lin last updated on 01/Jul/19
![∵ abc+(1−a)(1−b)(1−c)≥ [(√(abc))+(√((1−a)(1−b)(1−c)))]^2 (using Cauchy′s inequality) (1−a)(1−b)(1−c)+abc =1−c−a−b+ac+bc+ab≤1 ∴ (√(abc))+(√((1−a)(1−b)(1−c)))≤1](https://www.tinkutara.com/question/Q63248.png)
$$\because\:{abc}+\left(\mathrm{1}−{a}\right)\left(\mathrm{1}−{b}\right)\left(\mathrm{1}−{c}\right)\geqslant \\ $$$$\left[\sqrt{{abc}}+\sqrt{\left(\mathrm{1}−{a}\right)\left(\mathrm{1}−{b}\right)\left(\mathrm{1}−{c}\right)}\right]^{\mathrm{2}} \\ $$$$\left({using}\:{Cauchy}'{s}\:{inequality}\right) \\ $$$$\left(\mathrm{1}−{a}\right)\left(\mathrm{1}−{b}\right)\left(\mathrm{1}−{c}\right)+{abc} \\ $$$$=\mathrm{1}−{c}−{a}−{b}+{ac}+{bc}+{ab}\leqslant\mathrm{1} \\ $$$$\therefore\:\sqrt{{abc}}+\sqrt{\left(\mathrm{1}−{a}\right)\left(\mathrm{1}−{b}\right)\left(\mathrm{1}−{c}\right)}\leqslant\mathrm{1} \\ $$
