Question Number 85620 by Roland Mbunwe last updated on 23/Mar/20
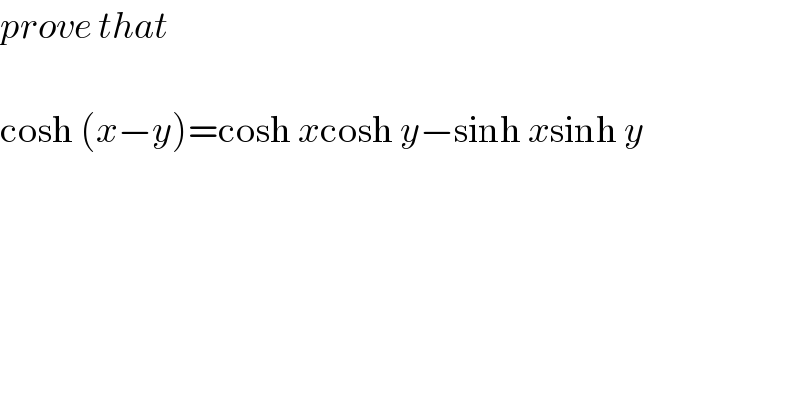
$${prove}\:{that} \\ $$$$ \\ $$$$\mathrm{cosh}\:\left({x}−{y}\right)=\mathrm{cosh}\:{x}\mathrm{cosh}\:{y}−\mathrm{sinh}\:{x}\mathrm{sinh}\:{y} \\ $$
Answered by Rio Michael last updated on 23/Mar/20
![RHS = cosh x cosh y − sinh x sinh y = (1/2)(e^x + e^(−x) ) (1/2)(e^y + e^(−y) ) − (1/2)(e^x −e^(−x) )(1/2)(e^y −e^(−y) ) = (1/4)[(e^x +e^(−x) )(e^y + e^(−y) )−(e^x −e^(−x) )(e^y −e^(−y) )] = (1/4)(2e^((x−y)) + 2e^(−(x−y)) ) = (1/2)(e^((x−y)) + e^(−(x−y)) ) = cosh(x−y)](https://www.tinkutara.com/question/Q85622.png)
$$\:{RHS}\:=\:\mathrm{cosh}\:{x}\:\mathrm{cosh}\:{y}\:−\:\mathrm{sinh}\:{x}\:\mathrm{sinh}\:{y} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left({e}^{{x}} \:+\:{e}^{−{x}} \right)\:\frac{\mathrm{1}}{\mathrm{2}}\left({e}^{{y}} \:+\:{e}^{−{y}} \right)\:−\:\frac{\mathrm{1}}{\mathrm{2}}\left({e}^{{x}} \:−{e}^{−{x}} \right)\frac{\mathrm{1}}{\mathrm{2}}\left({e}^{{y}} −{e}^{−{y}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{4}}\left[\left({e}^{{x}} +{e}^{−{x}} \right)\left({e}^{{y}} \:+\:{e}^{−{y}} \right)−\left({e}^{{x}} −{e}^{−{x}} \right)\left({e}^{{y}} −{e}^{−{y}} \right)\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{2}{e}^{\left({x}−{y}\right)} +\:\mathrm{2}{e}^{−\left({x}−{y}\right)} \right)\:=\:\frac{\mathrm{1}}{\mathrm{2}}\left({e}^{\left({x}−{y}\right)} \:+\:{e}^{−\left({x}−{y}\right)} \right)\:=\:\mathrm{cosh}\left({x}−{y}\right) \\ $$
