Question Number 111879 by mathdave last updated on 05/Sep/20
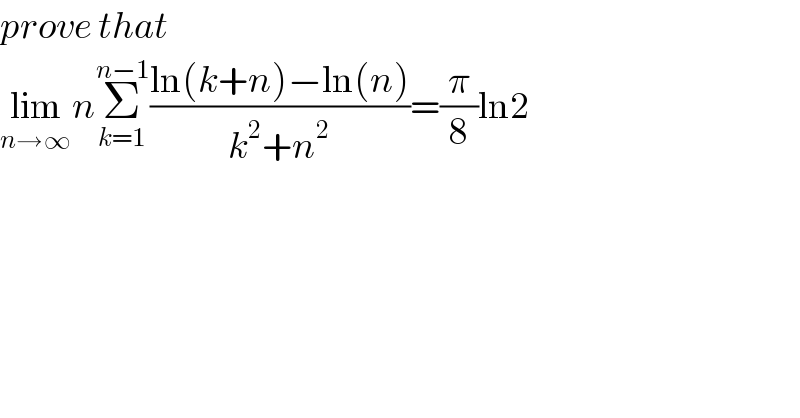
$${prove}\:{that}\: \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{n}\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\frac{\mathrm{ln}\left({k}+{n}\right)−\mathrm{ln}\left({n}\right)}{{k}^{\mathrm{2}} +{n}^{\mathrm{2}} }=\frac{\pi}{\mathrm{8}}\mathrm{ln2} \\ $$
Answered by Dwaipayan Shikari last updated on 05/Sep/20
![lim_(n→∞) nΣ_(k=0) ^n ((log((k/n)+1))/(k^2 +n^2 ))=lim_(n→∞) (1/n)Σ_(k=0) ^n ((log((k/n)+1))/((k^2 /n^2 )+1)) =∫_0 ^1 ((log(x+1))/(x^2 +1))dx =∫_0 ^(π/4) ((log(tanθ+1))/(tan^2 θ+1)).sec^2 θ dθ =∫_0 ^(π/4) log(sinθ+cosθ)−log(cosθ) =∫_0 ^(π/4) log((√2))+log(((sinθ+cosθ)/( (√2))))−log(cosθ) dθ =∫_0 ^(π/4) (1/2)log(2)+[∫_0 ^(π/4) log(cos((π/4)−θ)−log(cosθ))]=I =(π/8)log(2)+I=(π/8)log(2) ((∫_0 ^(π/4) log(cos((π/4)−θ))−log(cosθ)=∫_0 ^(π/4) log(cosθ)−log(cos((π/4)−θ))=I 2I=0))](https://www.tinkutara.com/question/Q111894.png)
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{n}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{{log}\left(\frac{{k}}{{n}}+\mathrm{1}\right)}{{k}^{\mathrm{2}} +{n}^{\mathrm{2}} }=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\frac{{log}\left(\frac{{k}}{{n}}+\mathrm{1}\right)}{\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{2}} }+\mathrm{1}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left({x}+\mathrm{1}\right)}{{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{log}\left({tan}\theta+\mathrm{1}\right)}{{tan}^{\mathrm{2}} \theta+\mathrm{1}}.{sec}^{\mathrm{2}} \theta\:{d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {log}\left({sin}\theta+{cos}\theta\right)−{log}\left({cos}\theta\right) \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {log}\left(\sqrt{\mathrm{2}}\right)+{log}\left(\frac{{sin}\theta+{cos}\theta}{\:\sqrt{\mathrm{2}}}\right)−{log}\left({cos}\theta\right)\:{d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{1}}{\mathrm{2}}{log}\left(\mathrm{2}\right)+\left[\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {log}\left({cos}\left(\frac{\pi}{\mathrm{4}}−\theta\right)−{log}\left({cos}\theta\right)\right)\right]={I} \\ $$$$=\frac{\pi}{\mathrm{8}}{log}\left(\mathrm{2}\right)+{I}=\frac{\pi}{\mathrm{8}}{log}\left(\mathrm{2}\right) \\ $$$$\left(\left(\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {log}\left({cos}\left(\frac{\pi}{\mathrm{4}}−\theta\right)\right)−{log}\left({cos}\theta\right)=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {log}\left({cos}\theta\right)−{log}\left({cos}\left(\frac{\pi}{\mathrm{4}}−\theta\right)\right)={I}\right.\right. \\ $$$$\left.\mathrm{2}\left.{I}=\mathrm{0}\right)\right) \\ $$
Commented by mathdave last updated on 05/Sep/20
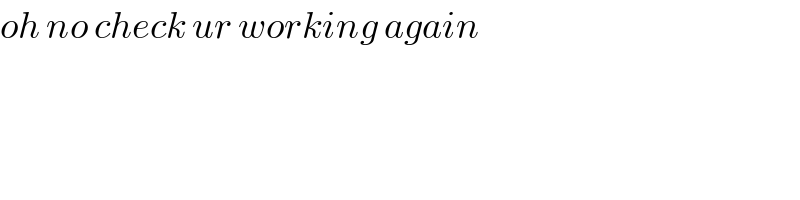
$${oh}\:{no}\:{check}\:{ur}\:{working}\:{again} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 05/Sep/20
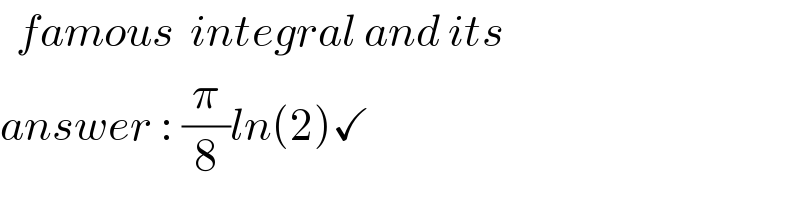
$$\:\:{famous}\:\:{integral}\:{and}\:{its} \\ $$$${answer}\::\:\frac{\pi}{\mathrm{8}}{ln}\left(\mathrm{2}\right)\checkmark \\ $$
Commented by mathdave last updated on 05/Sep/20
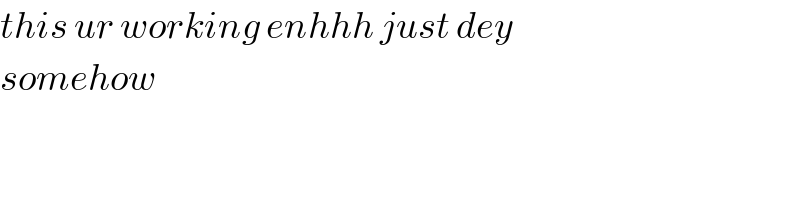
$${this}\:{ur}\:{working}\:{enhhh}\:{just}\:{dey} \\ $$$${somehow}\: \\ $$
