Question Number 54371 by maxmathsup by imad last updated on 02/Feb/19
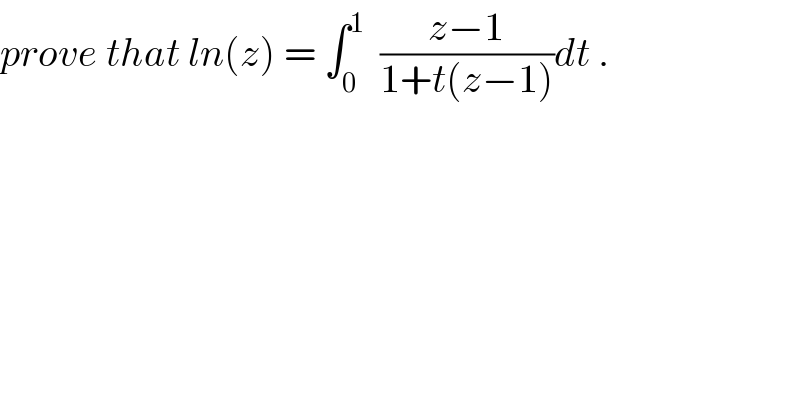
$${prove}\:{that}\:{ln}\left({z}\right)\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{z}−\mathrm{1}}{\mathrm{1}+{t}\left({z}−\mathrm{1}\right)}{dt}\:. \\ $$
Commented by maxmathsup by imad last updated on 02/Feb/19
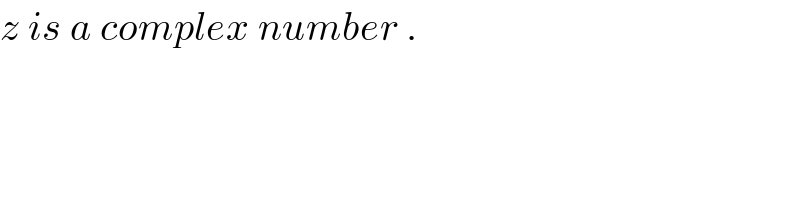
$${z}\:{is}\:{a}\:{complex}\:{number}\:. \\ $$
Answered by Smail last updated on 02/Feb/19
![let u=t(z−1)⇒du=(z−1)dt ∫_0 ^1 ((z−1)/(1+t(z−1)))dt=∫_0 ^(z−1) (du/(1+u))=[ln∣1+u∣]_0 ^(z−1) =ln∣1+z−1∣=ln∣z∣](https://www.tinkutara.com/question/Q54375.png)
$${let}\:\:{u}={t}\left({z}−\mathrm{1}\right)\Rightarrow{du}=\left({z}−\mathrm{1}\right){dt} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{z}−\mathrm{1}}{\mathrm{1}+{t}\left({z}−\mathrm{1}\right)}{dt}=\int_{\mathrm{0}} ^{{z}−\mathrm{1}} \frac{{du}}{\mathrm{1}+{u}}=\left[{ln}\mid\mathrm{1}+{u}\mid\right]_{\mathrm{0}} ^{{z}−\mathrm{1}} \\ $$$$={ln}\mid\mathrm{1}+{z}−\mathrm{1}\mid={ln}\mid{z}\mid \\ $$
Commented by Abdo msup. last updated on 03/Feb/19
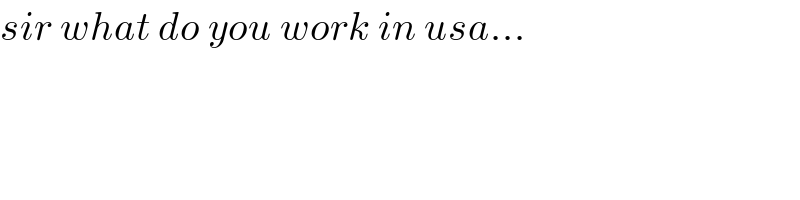
$${sir}\:{what}\:{do}\:{you}\:{work}\:{in}\:{usa}… \\ $$
Commented by Smail last updated on 03/Feb/19
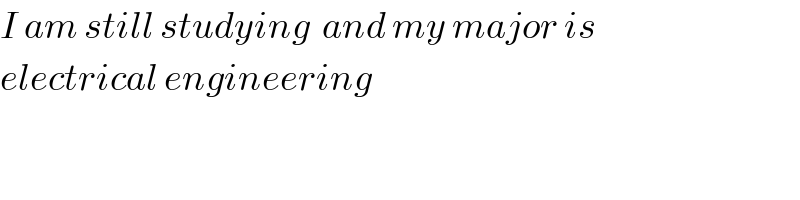
$${I}\:{am}\:{still}\:{studying}\:\:{and}\:{my}\:{major}\:{is}\: \\ $$$${electrical}\:{engineering} \\ $$
Commented by rahul 19 last updated on 03/Feb/19
$${wow}!\:{which}\:{university}? \\ $$
Commented by maxmathsup by imad last updated on 03/Feb/19
$${good}\:{luck}\:{sir}\:{Smail}…{i}\:{hoppe}\:{to}\:{visit}\:{usa}\:{somedays}… \\ $$
Commented by Smail last updated on 03/Feb/19

$${Thank}\:{you} \\ $$
