Question Number 101439 by mhmd last updated on 02/Jul/20

Commented by mhmd last updated on 02/Jul/20

$${help}\:{me}\:{sir}\:? \\ $$
Commented by bramlex last updated on 02/Jul/20
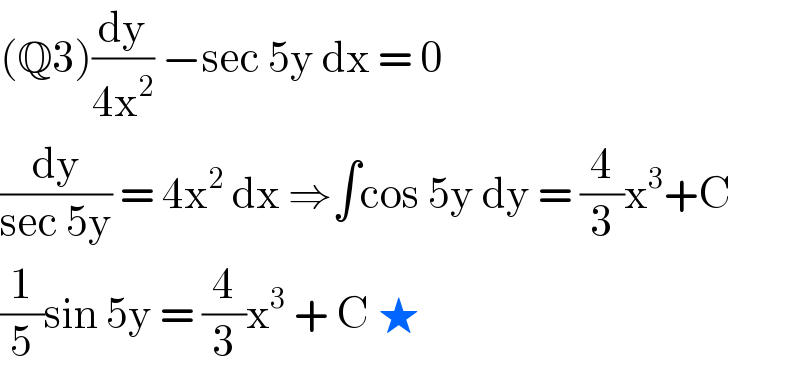
$$\left(\mathbb{Q}\mathrm{3}\right)\frac{\mathrm{dy}}{\mathrm{4x}^{\mathrm{2}} }\:−\mathrm{sec}\:\mathrm{5y}\:\mathrm{dx}\:=\:\mathrm{0} \\ $$$$\frac{\mathrm{dy}}{\mathrm{sec}\:\mathrm{5y}}\:=\:\mathrm{4x}^{\mathrm{2}} \:\mathrm{dx}\:\Rightarrow\int\mathrm{cos}\:\mathrm{5y}\:\mathrm{dy}\:=\:\frac{\mathrm{4}}{\mathrm{3}}\mathrm{x}^{\mathrm{3}} +\mathrm{C} \\ $$$$\frac{\mathrm{1}}{\mathrm{5}}\mathrm{sin}\:\mathrm{5y}\:=\:\frac{\mathrm{4}}{\mathrm{3}}\mathrm{x}^{\mathrm{3}} \:+\:\mathrm{C}\:\bigstar \\ $$
Commented by bemath last updated on 02/Jul/20
![(q4) 8x^2 = 32 , x = ± 2 The area = 2∫_0 ^2 (32−8x^2 ) dx = 2[(32x−(8/3)x^3 )]_0 ^2 = 2 (64−((64)/3)) = 128(1−(1/3)) = 128×(2/3) = ((256)/3) ♠](https://www.tinkutara.com/question/Q101442.png)
$$\left(\mathfrak{q}\mathrm{4}\right)\:\mathrm{8x}^{\mathrm{2}} \:=\:\mathrm{32}\:,\:\mathrm{x}\:=\:\pm\:\mathrm{2}\: \\ $$$$\mathcal{T}\mathrm{he}\:\mathrm{area}\:=\:\mathrm{2}\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\:\left(\mathrm{32}−\mathrm{8x}^{\mathrm{2}} \right)\:\mathrm{dx} \\ $$$$=\:\mathrm{2}\left[\left(\mathrm{32x}−\frac{\mathrm{8}}{\mathrm{3}}\mathrm{x}^{\mathrm{3}} \right)\right]_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$=\:\mathrm{2}\:\left(\mathrm{64}−\frac{\mathrm{64}}{\mathrm{3}}\right)\:=\:\mathrm{128}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$=\:\mathrm{128}×\frac{\mathrm{2}}{\mathrm{3}}\:=\:\frac{\mathrm{256}}{\mathrm{3}}\:\spadesuit \\ $$
Commented by mhmd last updated on 02/Jul/20

$${thank}\:{you}\:{sir} \\ $$
Commented by bemath last updated on 04/Jul/20
![(q2) ∫_0 ^2 [( 4y+(1/4)sin 4y)]_0 ^( π) dx =∫_0 ^2 (4π) dx = [ 4πy ]_0 ^2 = 8π ★](https://www.tinkutara.com/question/Q101444.png)
$$\left(\mathrm{q2}\right)\:\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\:\left[\left(\:\mathrm{4y}+\frac{\mathrm{1}}{\mathrm{4}}\mathrm{sin}\:\mathrm{4y}\right)\underset{\mathrm{0}} {\overset{\:\pi} {\right]}}\mathrm{dx}\: \\ $$$$=\underset{\mathrm{0}} {\overset{\mathrm{2}} {\int}}\:\left(\mathrm{4}\pi\right)\:\mathrm{dx}\:=\:\:\left[\:\mathrm{4}\pi\mathrm{y}\:\right]_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$=\:\mathrm{8}\pi\:\bigstar \\ $$
Commented by mhmd last updated on 02/Jul/20
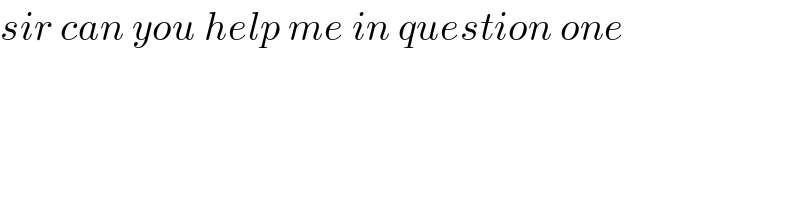
$${sir}\:{can}\:{you}\:{help}\:{me}\:{in}\:{question}\:{one} \\ $$
Commented by bobhans last updated on 02/Jul/20
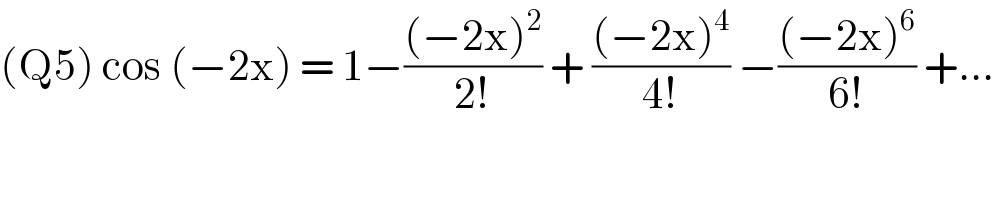
$$\left(\mathrm{Q5}\right)\:\mathrm{cos}\:\left(−\mathrm{2x}\right)\:=\:\mathrm{1}−\frac{\left(−\mathrm{2x}\right)^{\mathrm{2}} }{\mathrm{2}!}\:+\:\frac{\left(−\mathrm{2x}\right)^{\mathrm{4}} }{\mathrm{4}!}\:−\frac{\left(−\mathrm{2x}\right)^{\mathrm{6}} }{\mathrm{6}!}\:+… \\ $$
Commented by mhmd last updated on 02/Jul/20
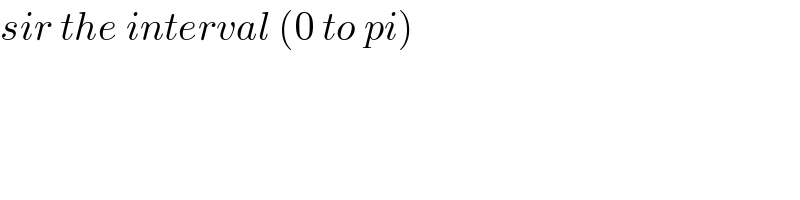
$${sir}\:{the}\:{interval}\:\left(\mathrm{0}\:{to}\:{pi}\right) \\ $$
Commented by mhmd last updated on 02/Jul/20
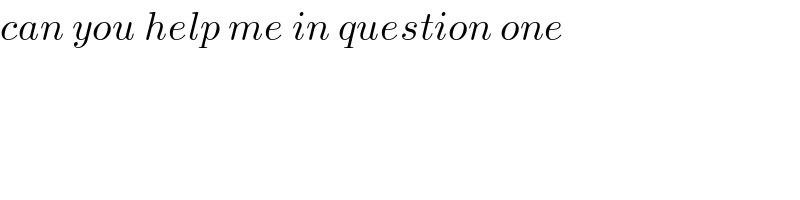
$${can}\:{you}\:{help}\:{me}\:{in}\:{question}\:{one} \\ $$
Commented by mhmd last updated on 03/Jul/20
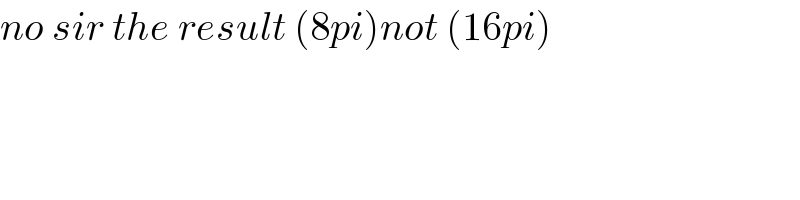
$${no}\:{sir}\:{the}\:{result}\:\left(\mathrm{8}{pi}\right){not}\:\left(\mathrm{16}{pi}\right) \\ $$
