Menu Close

Question-101546

Tinku Tara 0 Comments
Pin




Question Number 101546 by mhmd last updated on 03/Jul/20
Commented by mhmd last updated on 03/Jul/20
help me sir
$${help}\:{me}\:{sir} \\ $$
Answered by bobhans last updated on 03/Jul/20
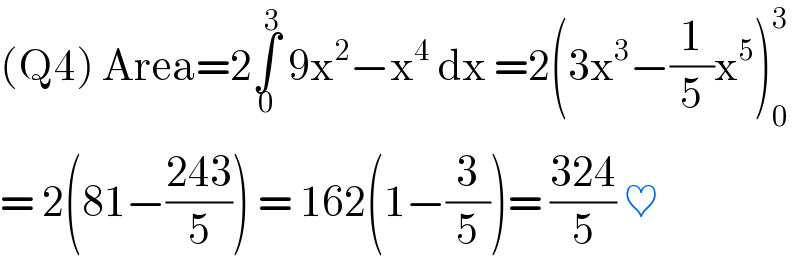
(Q4) Area=2∫_0 ^3 9x^2 −x^4 dx =2(3x^3 −(1/5)x^5 )_0 ^3 = 2(81−((243)/5)) = 162(1−(3/5))= ((324)/5) ♥
$$\left(\mathrm{Q4}\right)\:\mathrm{Area}=\mathrm{2}\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\:\mathrm{9x}^{\mathrm{2}} −\mathrm{x}^{\mathrm{4}} \:\mathrm{dx}\:=\mathrm{2}\left(\mathrm{3x}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{5}}\mathrm{x}^{\mathrm{5}} \right)_{\mathrm{0}} ^{\mathrm{3}} \\ $$$$=\:\mathrm{2}\left(\mathrm{81}−\frac{\mathrm{243}}{\mathrm{5}}\right)\:=\:\mathrm{162}\left(\mathrm{1}−\frac{\mathrm{3}}{\mathrm{5}}\right)=\:\frac{\mathrm{324}}{\mathrm{5}}\:\heartsuit \\ $$
Commented by mhmd last updated on 03/Jul/20
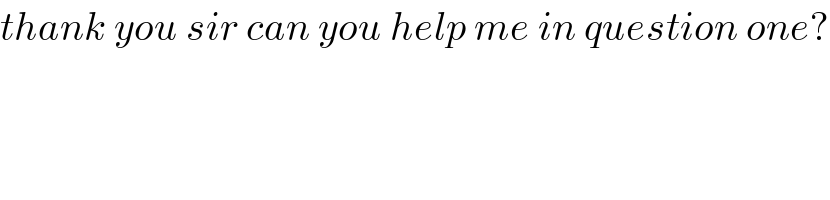
thank you sir can you help me in question one?
$${thank}\:{you}\:{sir}\:{can}\:{you}\:{help}\:{me}\:{in}\:{question}\:{one}? \\ $$
Answered by john santu last updated on 03/Jul/20
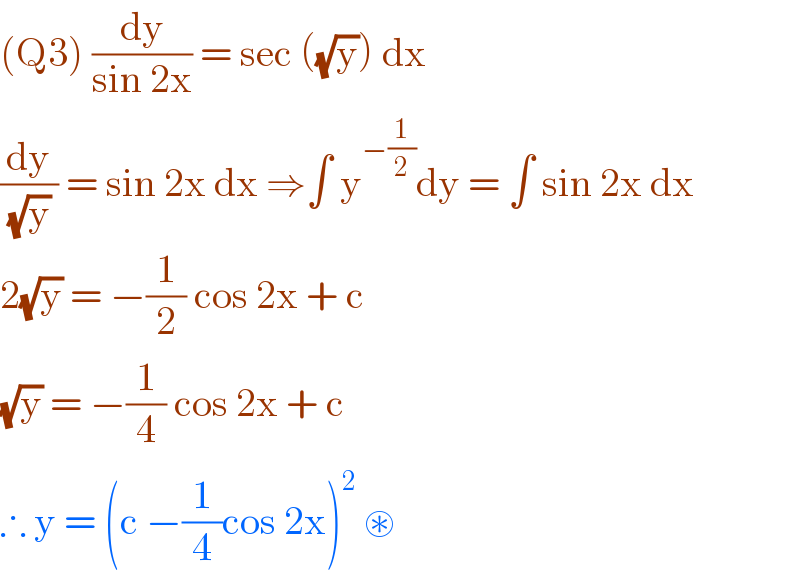
(Q3) (dy/(sin 2x)) = sec ((√y)) dx (dy/( (√y) )) = sin 2x dx ⇒∫ y^(−(1/2)) dy = ∫ sin 2x dx 2(√y) = −(1/2) cos 2x + c (√y) = −(1/4) cos 2x + c ∴ y = (c −(1/4)cos 2x)^2 ⊛
$$\left(\mathrm{Q3}\right)\:\frac{\mathrm{dy}}{\mathrm{sin}\:\mathrm{2x}}\:=\:\mathrm{sec}\:\left(\sqrt{\mathrm{y}}\right)\:\mathrm{dx} \\ $$$$\frac{\mathrm{dy}}{\:\sqrt{\mathrm{y}}\:}\:=\:\mathrm{sin}\:\mathrm{2x}\:\mathrm{dx}\:\Rightarrow\int\:\mathrm{y}^{−\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{dy}\:=\:\int\:\mathrm{sin}\:\mathrm{2x}\:\mathrm{dx} \\ $$$$\mathrm{2}\sqrt{\mathrm{y}}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{cos}\:\mathrm{2x}\:+\:\mathrm{c}\: \\ $$$$\sqrt{\mathrm{y}}\:=\:−\frac{\mathrm{1}}{\mathrm{4}}\:\mathrm{cos}\:\mathrm{2x}\:+\:\mathrm{c}\: \\ $$$$\therefore\:\mathrm{y}\:=\:\left(\mathrm{c}\:−\frac{\mathrm{1}}{\mathrm{4}}\mathrm{cos}\:\mathrm{2x}\right)^{\mathrm{2}} \:\circledast\: \\ $$
Answered by abdomathmax last updated on 03/Jul/20
Q_2 ) ∫_0 ^2 (∫_0 ^(2π) (5ysin(5y)+xe^x )dydx =∫_0 ^2 A(x)dx with A(x) =∫_0 ^(2π) (5ysin(5y)+xe^x )dy A(x) =5 ∫_0 ^(2π) ysin(5y)dy +2πxe^x =5{ [−(y/5)cos(5y)]_0 ^(2π) +(1/5)∫_0 ^(2π) cos(5y)dy}+2πxe^x =5{−((2π)/5) +(1/(25))[sin(5y)]_0 ^(2π) } +2πxe^x =−2π +2πxe^x ⇒ I =∫_0 ^2 (−2π+2πxe^x )dx =−4π +2π ∫_0 ^2 xe^x dx =−4π +2π{ [xe^x ]_0 ^2 −∫_0 ^2 e^x dx} =−4π +2π{2e^2 −(e^2 −1)} =−4π +2π{e^2 +1) =−2π +2πe^2
$$\left.\mathrm{Q}_{\mathrm{2}} \right)\:\:\:\:\int_{\mathrm{0}} ^{\mathrm{2}} \:\left(\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left(\mathrm{5ysin}\left(\mathrm{5y}\right)+\mathrm{xe}^{\mathrm{x}} \right)\mathrm{dydx}\right. \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{2}} \mathrm{A}\left(\mathrm{x}\right)\mathrm{dx}\:\mathrm{with}\:\mathrm{A}\left(\mathrm{x}\right)\:=\int_{\mathrm{0}} ^{\mathrm{2}\pi} \left(\mathrm{5ysin}\left(\mathrm{5y}\right)+\mathrm{xe}^{\mathrm{x}} \right)\mathrm{dy} \\ $$$$\mathrm{A}\left(\mathrm{x}\right)\:=\mathrm{5}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:\mathrm{ysin}\left(\mathrm{5y}\right)\mathrm{dy}\:+\mathrm{2}\pi\mathrm{xe}^{\mathrm{x}} \\ $$$$=\mathrm{5}\left\{\:\left[−\frac{\mathrm{y}}{\mathrm{5}}\mathrm{cos}\left(\mathrm{5y}\right)\right]_{\mathrm{0}} ^{\mathrm{2}\pi} +\frac{\mathrm{1}}{\mathrm{5}}\int_{\mathrm{0}} ^{\mathrm{2}\pi} \mathrm{cos}\left(\mathrm{5y}\right)\mathrm{dy}\right\}+\mathrm{2}\pi\mathrm{xe}^{\mathrm{x}} \\ $$$$=\mathrm{5}\left\{−\frac{\mathrm{2}\pi}{\mathrm{5}}\:+\frac{\mathrm{1}}{\mathrm{25}}\left[\mathrm{sin}\left(\mathrm{5y}\right)\right]_{\mathrm{0}} ^{\mathrm{2}\pi} \right\}\:+\mathrm{2}\pi\mathrm{xe}^{\mathrm{x}} \\ $$$$=−\mathrm{2}\pi\:+\mathrm{2}\pi\mathrm{xe}^{\mathrm{x}} \:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{2}} \left(−\mathrm{2}\pi+\mathrm{2}\pi\mathrm{xe}^{\mathrm{x}} \right)\mathrm{dx}\:=−\mathrm{4}\pi\:+\mathrm{2}\pi\:\int_{\mathrm{0}} ^{\mathrm{2}} \:\mathrm{xe}^{\mathrm{x}} \:\mathrm{dx} \\ $$$$=−\mathrm{4}\pi\:+\mathrm{2}\pi\left\{\:\left[\mathrm{xe}^{\mathrm{x}} \right]_{\mathrm{0}} ^{\mathrm{2}} −\int_{\mathrm{0}} ^{\mathrm{2}} \:\mathrm{e}^{\mathrm{x}} \mathrm{dx}\right\} \\ $$$$=−\mathrm{4}\pi\:+\mathrm{2}\pi\left\{\mathrm{2e}^{\mathrm{2}} −\left(\mathrm{e}^{\mathrm{2}} −\mathrm{1}\right)\right\} \\ $$$$=−\mathrm{4}\pi\:+\mathrm{2}\pi\left\{\mathrm{e}^{\mathrm{2}} \:+\mathrm{1}\right) \\ $$$$=−\mathrm{2}\pi\:+\mathrm{2}\pi\mathrm{e}^{\mathrm{2}} \\ $$$$ \\ $$
Answered by john santu last updated on 04/Jul/20
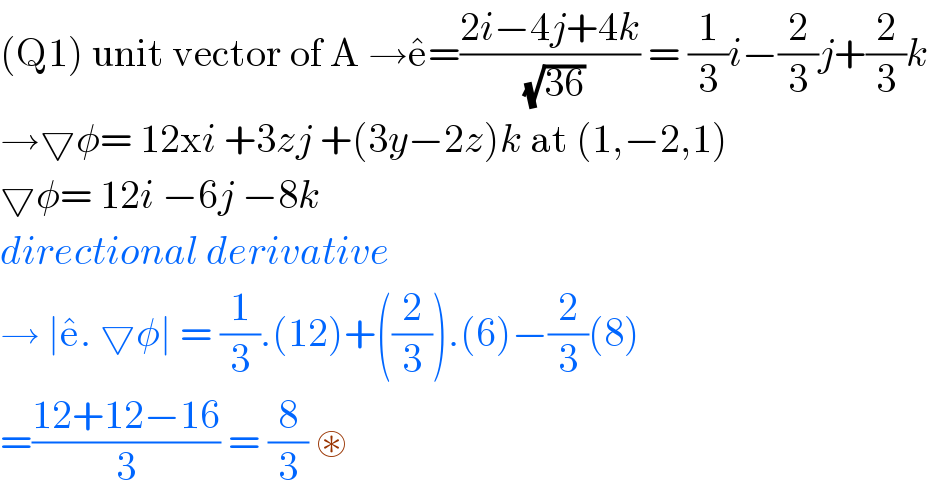
(Q1) unit vector of A →e^� =((2i−4j+4k)/( (√(36)))) = (1/3)i−(2/3)j+(2/3)k →▽φ= 12xi +3zj +(3y−2z)k at (1,−2,1) ▽φ= 12i −6j −8k directional derivative → ∣e^� . ▽φ∣ = (1/3).(12)+((2/3)).(6)−(2/3)(8) =((12+12−16)/3) = (8/3) ⊛
$$\left(\mathrm{Q1}\right)\:\mathrm{unit}\:\mathrm{vector}\:\mathrm{of}\:\mathrm{A}\:\rightarrow\hat {\mathrm{e}}=\frac{\mathrm{2}{i}−\mathrm{4}{j}+\mathrm{4}{k}}{\:\sqrt{\mathrm{36}}}\:=\:\frac{\mathrm{1}}{\mathrm{3}}{i}−\frac{\mathrm{2}}{\mathrm{3}}{j}+\frac{\mathrm{2}}{\mathrm{3}}{k} \\ $$$$\rightarrow\bigtriangledown\phi=\:\mathrm{12x}{i}\:+\mathrm{3}{zj}\:+\left(\mathrm{3}{y}−\mathrm{2}{z}\right){k}\:\mathrm{at}\:\left(\mathrm{1},−\mathrm{2},\mathrm{1}\right) \\ $$$$\bigtriangledown\phi=\:\mathrm{12}{i}\:−\mathrm{6}{j}\:−\mathrm{8}{k} \\ $$$${directional}\:{derivative}\: \\ $$$$\rightarrow\:\mid\hat {\mathrm{e}}.\:\bigtriangledown\phi\mid\:=\:\frac{\mathrm{1}}{\mathrm{3}}.\left(\mathrm{12}\right)+\left(\frac{\mathrm{2}}{\mathrm{3}}\right).\left(\mathrm{6}\right)−\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{8}\right) \\ $$$$=\frac{\mathrm{12}+\mathrm{12}−\mathrm{16}}{\mathrm{3}}\:=\:\frac{\mathrm{8}}{\mathrm{3}}\:\circledast\:\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *