Question Number 101551 by mhmd last updated on 03/Jul/20

Answered by bobhans last updated on 03/Jul/20
![(Q2) The area = ∫_0 ^1 ∫_0 ^x dy dx = ∫_0 ^1 (y)]_0 ^x dx = ∫_0 ^1 x dx = [ (1/2)x^2 ]_0 ^1 = (1/2) ♥](https://www.tinkutara.com/question/Q101572.png)
$$\left.\left(\mathrm{Q2}\right)\:\mathrm{The}\:\mathrm{area}\:=\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\underset{\mathrm{0}} {\overset{{x}} {\int}}\:{dy}\:{dx}\:=\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\left({y}\right)\right]_{\mathrm{0}} ^{{x}} \:\:{dx} \\ $$$$=\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:{x}\:{dx}\:=\:\:\left[\:\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \:\right]_{\mathrm{0}} ^{\mathrm{1}} =\:\frac{\mathrm{1}}{\mathrm{2}}\:\heartsuit \\ $$
Commented by mhmd last updated on 03/Jul/20
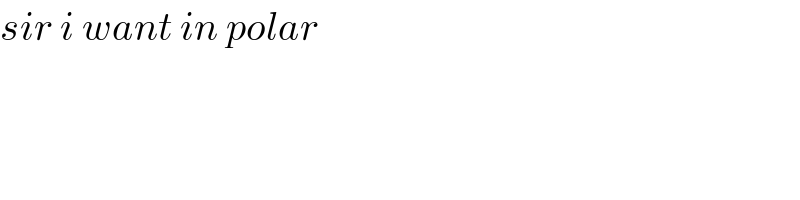
$${sir}\:{i}\:{want}\:{in}\:{polar} \\ $$
Answered by mr W last updated on 04/Jul/20
![Q2(b) 1−r cos θ=r sin θ ⇒r=(1/(sin θ+cos θ)) A=∫_0 ^(π/2) ∫_0 ^(1/(sin θ+cos θ)) ρdρdθ =(1/2)∫_0 ^(π/2) (1/((sin θ+cos θ)^2 ))dθ =(1/2)∫_0 ^(π/2) (1/(1+sin 2θ))dθ =(1/4)∫_0 ^(π/2) (1/(1+sin 2θ))d(2θ) =(1/4)∫_0 ^π (1/(1+sin t))dt =(1/4)[(2/(1+tan (t/2)))]_π ^0 =(1/2)(1−0) =(1/2)](https://www.tinkutara.com/question/Q101771.png)
$${Q}\mathrm{2}\left({b}\right) \\ $$$$\mathrm{1}−{r}\:\mathrm{cos}\:\theta={r}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow{r}=\frac{\mathrm{1}}{\mathrm{sin}\:\theta+\mathrm{cos}\:\theta} \\ $$$${A}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{sin}\:\theta+\mathrm{cos}\:\theta}} \rho{d}\rho{d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\left(\mathrm{sin}\:\theta+\mathrm{cos}\:\theta\right)^{\mathrm{2}} }{d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{1}+\mathrm{sin}\:\mathrm{2}\theta}{d}\theta \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\mathrm{1}}{\mathrm{1}+\mathrm{sin}\:\mathrm{2}\theta}{d}\left(\mathrm{2}\theta\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{1}}{\mathrm{1}+\mathrm{sin}\:{t}}{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left[\frac{\mathrm{2}}{\mathrm{1}+\mathrm{tan}\:\frac{{t}}{\mathrm{2}}}\right]_{\pi} ^{\mathrm{0}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{0}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
