Question Number 104101 by ajfour last updated on 19/Jul/20

Commented by ajfour last updated on 19/Jul/20

$${If}\:{the}\:{outer}\:{triangle}\:{is}\:{equilateral}, \\ $$$${and}\:{the}\:{two}\:{ellipses}\:{of}\:{same}\:{size} \\ $$$${and}\:{shape},\:{find}\:{ratio}\:{of}\:{area}\:{of} \\ $$$${outer}\:{triangle}\:{to}\:{inner}\left({blue}\right) \\ $$$${triangle}. \\ $$
Commented by mr W last updated on 19/Jul/20
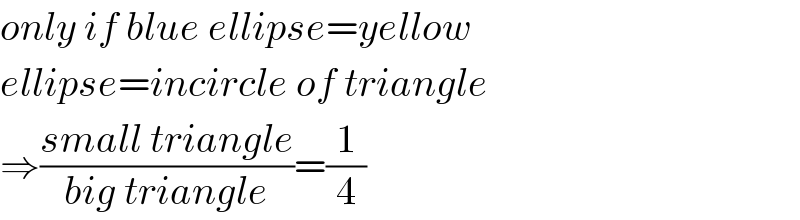
$${only}\:{if}\:{blue}\:{ellipse}={yellow} \\ $$$${ellipse}={incircle}\:{of}\:{triangle} \\ $$$$\Rightarrow\frac{{small}\:{triangle}}{{big}\:{triangle}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$
Answered by ajfour last updated on 19/Jul/20
![let eq. of blue ellipse be (x^2 /a^2 )+(((y−b)^2 )/b^2 )=1 Let right side of outer triangle has eq: y=x(√3)+c and as this is tangent to both ellipses, first b^2 x^2 +a^2 (x(√3)+c−b)^2 −a^2 b^2 =0 or (3a^2 +b^2 )x^2 +2(√3)(a^2 )(c−b)x +a^2 (c−b)^2 −a^2 b^2 =0 has double root; ⇒ 12a^4 (c−b)^2 =4a^2 (3a^2 +b^2 )[(c−b)^2 −b^2 ] ⇒ 3a^2 (c−b)^2 =(3a^2 +b^2 )[(c−b)^2 −b^2 ] ⇒ (c−b)^2 =3a^2 +b^2 .....(I) Now eq. of the yellow ellipse is (x^2 /b^2 )+(((y−a)^2 )/a^2 )=1 y=x(√3)+c is tangent to this ellipse too, hence a^2 x^2 +b^2 (x(√3)+c−a)^2 −a^2 b^2 =0 (a^2 +3b^2 )x^2 +2(√3)(b^2 )(c−a)x +b^2 [(c−a)^2 −a^2 ]=0 has also a double root; ⇒ 12b^4 (c−a)^2 =4b^2 (a^2 +3b^2 )[(c−a)^2 −a^2 ] ⇒ 3b^2 (c−a)^2 =(a^2 +3b^2 )[(c−a)^2 −a^2 ] ⇒ (c−a)^2 = a^2 +3b^2 .....(II) Now eliminating c among (I)&(II) b+(√(3a^2 +b^2 )) = a+(√(a^2 +3b^2 )) let (b/a) = μ ⇒ μ+(√(3+μ^2 ))=1+(√(1+3μ^2 )) ....(i) ⇒ μ=1 ★ ⇒ c−a = c−b = 2a =2b ⇒ a = b = (c/3) ⇒ (△_(small) /△_(large) ) = (1/4) ■ mrW Sir you are perfectly right!](https://www.tinkutara.com/question/Q104130.png)
$${let}\:{eq}.\:{of}\:{blue}\:{ellipse}\:{be} \\ $$$$\:\:\frac{\boldsymbol{{x}}^{\mathrm{2}} }{\boldsymbol{{a}}^{\mathrm{2}} }+\frac{\left(\boldsymbol{{y}}−\boldsymbol{{b}}\right)^{\mathrm{2}} }{\boldsymbol{{b}}^{\mathrm{2}} }=\mathrm{1} \\ $$$${Let}\:{right}\:{side}\:{of}\:{outer}\:{triangle}\:{has} \\ $$$${eq}:\:\:\:{y}={x}\sqrt{\mathrm{3}}+{c}\:\:\:\:\:\:{and}\:{as}\:{this}\:{is} \\ $$$${tangent}\:{to}\:{both}\:{ellipses},\:\:{first} \\ $$$$\:\:{b}^{\mathrm{2}} {x}^{\mathrm{2}} +{a}^{\mathrm{2}} \left({x}\sqrt{\mathrm{3}}+{c}−{b}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} =\mathrm{0} \\ $$$${or} \\ $$$$\:\:\left(\mathrm{3}{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right){x}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{3}}\left({a}^{\mathrm{2}} \right)\left({c}−{b}\right){x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{a}^{\mathrm{2}} \left({c}−{b}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} =\mathrm{0} \\ $$$${has}\:{double}\:{root};\:\:\Rightarrow \\ $$$$\mathrm{12}{a}^{\mathrm{4}} \left({c}−{b}\right)^{\mathrm{2}} =\mathrm{4}{a}^{\mathrm{2}} \left(\mathrm{3}{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left[\left({c}−{b}\right)^{\mathrm{2}} −{b}^{\mathrm{2}} \right] \\ $$$$\Rightarrow\:\mathrm{3}{a}^{\mathrm{2}} \left({c}−{b}\right)^{\mathrm{2}} =\left(\mathrm{3}{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\left[\left({c}−{b}\right)^{\mathrm{2}} −{b}^{\mathrm{2}} \right] \\ $$$$\Rightarrow\:\:\left({c}−{b}\right)^{\mathrm{2}} =\mathrm{3}{a}^{\mathrm{2}} +{b}^{\mathrm{2}} \:\:\:\:\:…..\left({I}\right) \\ $$$${Now}\:{eq}.\:{of}\:{the}\:{yellow}\:{ellipse}\:{is} \\ $$$$\:\:\:\:\:\:\frac{{x}^{\mathrm{2}} }{{b}^{\mathrm{2}} }+\frac{\left({y}−{a}\right)^{\mathrm{2}} }{{a}^{\mathrm{2}} }=\mathrm{1} \\ $$$${y}={x}\sqrt{\mathrm{3}}+{c}\:\:\:{is}\:{tangent}\:{to}\:{this}\:{ellipse} \\ $$$${too},\:\:{hence} \\ $$$$\:\:{a}^{\mathrm{2}} {x}^{\mathrm{2}} +{b}^{\mathrm{2}} \left({x}\sqrt{\mathrm{3}}+{c}−{a}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} {b}^{\mathrm{2}} =\mathrm{0} \\ $$$$\left({a}^{\mathrm{2}} +\mathrm{3}{b}^{\mathrm{2}} \right){x}^{\mathrm{2}} +\mathrm{2}\sqrt{\mathrm{3}}\left({b}^{\mathrm{2}} \right)\left({c}−{a}\right){x} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{b}^{\mathrm{2}} \left[\left({c}−{a}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} \right]=\mathrm{0} \\ $$$${has}\:{also}\:{a}\:{double}\:{root};\:\Rightarrow \\ $$$$\mathrm{12}{b}^{\mathrm{4}} \left({c}−{a}\right)^{\mathrm{2}} =\mathrm{4}{b}^{\mathrm{2}} \left({a}^{\mathrm{2}} +\mathrm{3}{b}^{\mathrm{2}} \right)\left[\left({c}−{a}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} \right] \\ $$$$\Rightarrow\:\:\mathrm{3}{b}^{\mathrm{2}} \left({c}−{a}\right)^{\mathrm{2}} =\left({a}^{\mathrm{2}} +\mathrm{3}{b}^{\mathrm{2}} \right)\left[\left({c}−{a}\right)^{\mathrm{2}} −{a}^{\mathrm{2}} \right] \\ $$$$\Rightarrow\:\:\left({c}−{a}\right)^{\mathrm{2}} =\:{a}^{\mathrm{2}} +\mathrm{3}{b}^{\mathrm{2}} \:\:\:\:\:…..\left({II}\right) \\ $$$${Now}\:{eliminating}\:{c}\:\:{among}\:\left({I}\right)\&\left({II}\right) \\ $$$$\:\:\:{b}+\sqrt{\mathrm{3}{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\:=\:{a}+\sqrt{{a}^{\mathrm{2}} +\mathrm{3}{b}^{\mathrm{2}} } \\ $$$${let}\:\:\:\frac{{b}}{{a}}\:=\:\mu \\ $$$$\Rightarrow\:\:\mu+\sqrt{\mathrm{3}+\mu^{\mathrm{2}} }=\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{3}\mu^{\mathrm{2}} }\:\:\:\:….\left(\boldsymbol{{i}}\right) \\ $$$$\Rightarrow\:\:\:\:\mu=\mathrm{1}\:\:\:\bigstar \\ $$$$\Rightarrow\:\:\:{c}−{a}\:=\:{c}−{b}\:=\:\mathrm{2}{a}\:=\mathrm{2}{b} \\ $$$$\Rightarrow\:\:\:{a}\:=\:{b}\:=\:\frac{{c}}{\mathrm{3}} \\ $$$$\Rightarrow\:\:\:\frac{\bigtriangleup_{{small}} }{\bigtriangleup_{{large}} }\:=\:\frac{\mathrm{1}}{\mathrm{4}}\:\blacksquare \\ $$$${mrW}\:{Sir}\:\:{you}\:{are}\:{perfectly}\:{right}! \\ $$
