Question Number 112133 by shwebotetun last updated on 06/Sep/20
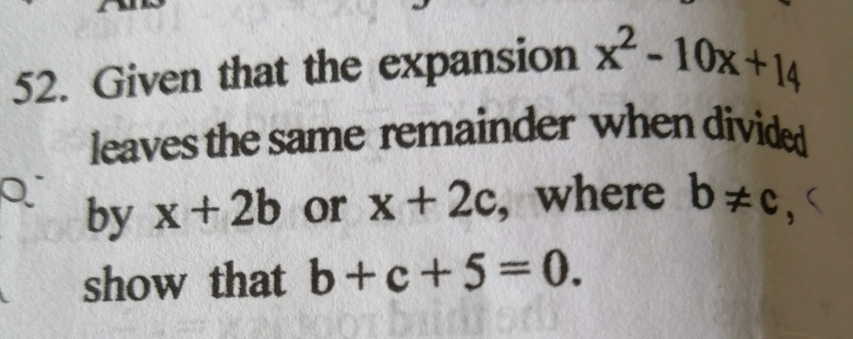
Answered by som(math1967) last updated on 06/Sep/20
![(−2b)^2 +20b+14=(−2c)^2 +20c+14 4b^2 −4c^2 +20(b−c)=0 4{(b−c)(b+c)+5(b−c)}=0 (b−c)(b+c+5)=0 ∴b+c+5=0 [∵b≠c ∴(b−c)≠0]](https://www.tinkutara.com/question/Q112134.png)
$$\left(−\mathrm{2b}\right)^{\mathrm{2}} +\mathrm{20b}+\mathrm{14}=\left(−\mathrm{2c}\right)^{\mathrm{2}} +\mathrm{20c}+\mathrm{14} \\ $$$$\mathrm{4b}^{\mathrm{2}} −\mathrm{4c}^{\mathrm{2}} +\mathrm{20}\left(\mathrm{b}−\mathrm{c}\right)=\mathrm{0} \\ $$$$\mathrm{4}\left\{\left(\mathrm{b}−\mathrm{c}\right)\left(\mathrm{b}+\mathrm{c}\right)+\mathrm{5}\left(\mathrm{b}−\mathrm{c}\right)\right\}=\mathrm{0} \\ $$$$\left(\mathrm{b}−\mathrm{c}\right)\left(\mathrm{b}+\mathrm{c}+\mathrm{5}\right)=\mathrm{0} \\ $$$$\therefore\mathrm{b}+\mathrm{c}+\mathrm{5}=\mathrm{0}\:\left[\because\mathrm{b}\neq\mathrm{c}\:\therefore\left(\mathrm{b}−\mathrm{c}\right)\neq\mathrm{0}\right] \\ $$
