Question Number 112403 by ajfour last updated on 07/Sep/20
Commented by ajfour last updated on 07/Sep/20

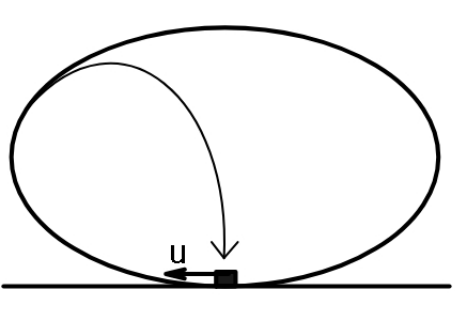
$${The}\:{elliptical}\:{frictionless}\:{track}\:{has} \\ $$$$\:{axes}\:{lengths}\:\boldsymbol{{a}},\:\:\boldsymbol{{b}}. \\ $$$${Find}\:{initial}\:{speed}\:\boldsymbol{{u}},\:{that}\:{must}\:{be} \\ $$$${given}\:{to}\:{a}\:{block}\:{such}\:{that}\:{its} \\ $$$${trajectory}\:{is}\:{as}\:{depicted}. \\ $$
Answered by mr W last updated on 07/Sep/20

Commented by mr W last updated on 08/Sep/20
![P(−h, k) h=a cos ϕ k=b sin ϕ tan θ=(b/(a tan ϕ))=(μ/(tan ϕ)) ((mu^2 )/2)=((mv^2 )/2)+mg(b+k) ⇒u^2 =v^2 +2μga(1+sin ϕ) t=(h/(v cos θ)) k+b=−v sin θ×(h/(v cos θ))+(1/2)g((h/(v cos θ)))^2 k+b=−h tan θ+((gh^2 (1+tan^2 θ))/(2v^2 )) ⇒(v^2 /(ga))=((sin ϕ (1−sin ϕ))/(2μ))(1−μ^2 +(μ^2 /(sin^2 ϕ))) y′=(μ/(tan ϕ)) y′′=((dy′)/dx)=((dy′)/dϕ)×(1/(dx/dϕ))=−(μ/(a sin^3 ϕ)) R=∣(((1+y′^2 )^(3/2) )/(y′′))∣ R=((a sin^3 ϕ(1+(μ^2 /(tan^2 ϕ)))^(3/2) )/μ) mg cos θ=((mv^2 )/R) (√(1/(1+(μ^2 /(tan^2 ϕ)))))=((μ[((sin ϕ (1−sin ϕ))/(2μ))(1−μ^2 +(μ^2 /(sin^2 ϕ)))])/(sin^3 ϕ(1+(μ^2 /(tan^2 ϕ)))^(3/2) )) ⇒2(1+sin ϕ)(μ^2 +tan^2 ϕ)=1−μ^2 +(μ^2 /(sin^2 ϕ)) ⇒2sin^2 ϕ[μ^2 +(1−μ^2 )sin^2 ϕ]=(1−sin ϕ)[μ^2 +(1−μ^2 )sin^2 ϕ] ⇒(2sin^2 ϕ+sin ϕ−1)[μ^2 +(1−μ^2 )sin^2 ϕ]=0 ⇒2sin^2 ϕ+sin ϕ−1=0 ⇒(2 sin ϕ−1)(sin ϕ+1)=0 ⇒sin ϕ=(1/2)⇒ϕ=(π/6)for any μ. ⇒(v^2 /(ga))=(( 1+3μ^2 )/(8μ)) ⇒(u^2 /(ga))=((1+27μ^2 )/(8μ))](https://www.tinkutara.com/question/Q112433.png)
$${P}\left(−{h},\:{k}\right) \\ $$$${h}={a}\:\mathrm{cos}\:\varphi \\ $$$${k}={b}\:\mathrm{sin}\:\varphi \\ $$$$\mathrm{tan}\:\theta=\frac{{b}}{{a}\:\mathrm{tan}\:\varphi}=\frac{\mu}{\mathrm{tan}\:\varphi} \\ $$$$\frac{{mu}^{\mathrm{2}} }{\mathrm{2}}=\frac{{mv}^{\mathrm{2}} }{\mathrm{2}}+{mg}\left({b}+{k}\right) \\ $$$$\Rightarrow{u}^{\mathrm{2}} ={v}^{\mathrm{2}} +\mathrm{2}\mu{ga}\left(\mathrm{1}+\mathrm{sin}\:\varphi\right) \\ $$$${t}=\frac{{h}}{{v}\:\mathrm{cos}\:\theta} \\ $$$${k}+{b}=−{v}\:\mathrm{sin}\:\theta×\frac{{h}}{{v}\:\mathrm{cos}\:\theta}+\frac{\mathrm{1}}{\mathrm{2}}{g}\left(\frac{{h}}{{v}\:\mathrm{cos}\:\theta}\right)^{\mathrm{2}} \\ $$$${k}+{b}=−{h}\:\mathrm{tan}\:\theta+\frac{{gh}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \:\theta\right)}{\mathrm{2}{v}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{{v}^{\mathrm{2}} }{{ga}}=\frac{\mathrm{sin}\:\varphi\:\left(\mathrm{1}−\mathrm{sin}\:\varphi\right)}{\mathrm{2}\mu}\left(\mathrm{1}−\mu^{\mathrm{2}} +\frac{\mu^{\mathrm{2}} }{\mathrm{sin}^{\mathrm{2}} \:\varphi}\right) \\ $$$$ \\ $$$${y}'=\frac{\mu}{\mathrm{tan}\:\varphi} \\ $$$${y}''=\frac{{dy}'}{{dx}}=\frac{{dy}'}{{d}\varphi}×\frac{\mathrm{1}}{\frac{{dx}}{{d}\varphi}}=−\frac{\mu}{{a}\:\mathrm{sin}^{\mathrm{3}} \:\varphi} \\ $$$${R}=\mid\frac{\left(\mathrm{1}+{y}'^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{{y}''}\mid \\ $$$${R}=\frac{{a}\:\mathrm{sin}^{\mathrm{3}} \:\varphi\left(\mathrm{1}+\frac{\mu^{\mathrm{2}} }{\mathrm{tan}^{\mathrm{2}} \:\varphi}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{\mu} \\ $$$${mg}\:\mathrm{cos}\:\theta=\frac{{mv}^{\mathrm{2}} }{{R}} \\ $$$$\sqrt{\frac{\mathrm{1}}{\mathrm{1}+\frac{\mu^{\mathrm{2}} }{\mathrm{tan}^{\mathrm{2}} \:\varphi}}}=\frac{\mu\left[\frac{\mathrm{sin}\:\varphi\:\left(\mathrm{1}−\mathrm{sin}\:\varphi\right)}{\mathrm{2}\mu}\left(\mathrm{1}−\mu^{\mathrm{2}} +\frac{\mu^{\mathrm{2}} }{\mathrm{sin}^{\mathrm{2}} \:\varphi}\right)\right]}{\mathrm{sin}^{\mathrm{3}} \:\varphi\left(\mathrm{1}+\frac{\mu^{\mathrm{2}} }{\mathrm{tan}^{\mathrm{2}} \:\varphi}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$\Rightarrow\mathrm{2}\left(\mathrm{1}+\mathrm{sin}\:\varphi\right)\left(\mu^{\mathrm{2}} +\mathrm{tan}^{\mathrm{2}} \:\varphi\right)=\mathrm{1}−\mu^{\mathrm{2}} +\frac{\mu^{\mathrm{2}} }{\mathrm{sin}^{\mathrm{2}} \:\varphi} \\ $$$$\Rightarrow\mathrm{2sin}^{\mathrm{2}} \:\varphi\left[\mu^{\mathrm{2}} +\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\mathrm{sin}^{\mathrm{2}} \:\varphi\right]=\left(\mathrm{1}−\mathrm{sin}\:\varphi\right)\left[\mu^{\mathrm{2}} +\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\mathrm{sin}^{\mathrm{2}} \:\varphi\right] \\ $$$$\Rightarrow\left(\mathrm{2sin}^{\mathrm{2}} \:\varphi+\mathrm{sin}\:\varphi−\mathrm{1}\right)\left[\mu^{\mathrm{2}} +\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\mathrm{sin}^{\mathrm{2}} \:\varphi\right]=\mathrm{0} \\ $$$$\Rightarrow\mathrm{2sin}^{\mathrm{2}} \:\varphi+\mathrm{sin}\:\varphi−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{2}\:\mathrm{sin}\:\varphi−\mathrm{1}\right)\left(\mathrm{sin}\:\varphi+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{sin}\:\varphi=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\varphi=\frac{\pi}{\mathrm{6}}{for}\:{any}\:\mu. \\ $$$$\Rightarrow\frac{{v}^{\mathrm{2}} }{{ga}}=\frac{\:\mathrm{1}+\mathrm{3}\mu^{\mathrm{2}} }{\mathrm{8}\mu} \\ $$$$\Rightarrow\frac{{u}^{\mathrm{2}} }{{ga}}=\frac{\mathrm{1}+\mathrm{27}\mu^{\mathrm{2}} }{\mathrm{8}\mu} \\ $$
Commented by mr W last updated on 08/Sep/20
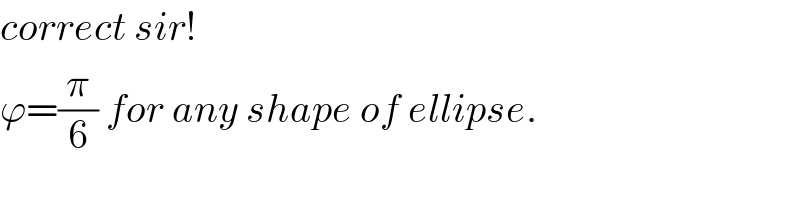
$${correct}\:{sir}! \\ $$$$\varphi=\frac{\pi}{\mathrm{6}}\:{for}\:{any}\:{shape}\:{of}\:{ellipse}. \\ $$
Commented by mr W last updated on 08/Sep/20
Commented by mr W last updated on 08/Sep/20
Commented by ajfour last updated on 08/Sep/20
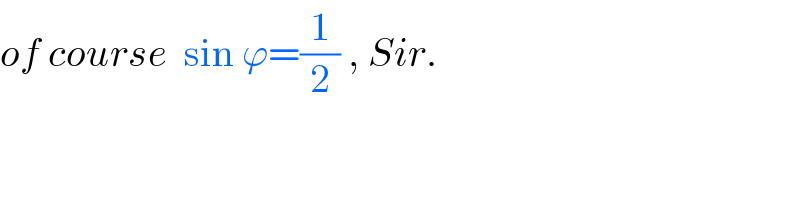
$${of}\:{course}\:\:\mathrm{sin}\:\varphi=\frac{\mathrm{1}}{\mathrm{2}}\:,\:{Sir}. \\ $$
Commented by ajfour last updated on 08/Sep/20
![If μ^2 +(1−μ^2 )sin^2 ϕ=0 μ > 1 , Sir. And sir please explain me R= (( [1+((dy/dx))^2 ]^(3/2) )/(−((d^2 y/dx^2 ))))](https://www.tinkutara.com/question/Q112598.png)
$${If}\:\:\mu^{\mathrm{2}} +\left(\mathrm{1}−\mu^{\mathrm{2}} \right)\mathrm{sin}^{\mathrm{2}} \:\varphi=\mathrm{0} \\ $$$$\mu\:>\:\mathrm{1}\:,\:{Sir}. \\ $$$${And}\:{sir}\:{please}\:{explain}\:{me} \\ $$$${R}=\:\frac{\:\:\:\left[\mathrm{1}+\left(\frac{{dy}}{{dx}}\right)^{\mathrm{2}} \:\right]^{\mathrm{3}/\mathrm{2}} }{−\left(\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\right)} \\ $$
Commented by mr W last updated on 08/Sep/20

Commented by mr W last updated on 08/Sep/20
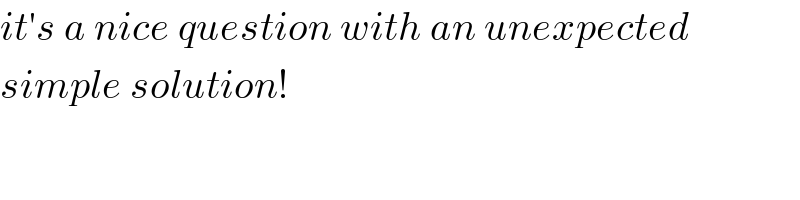
$${it}'{s}\:{a}\:{nice}\:{question}\:{with}\:{an}\:{unexpected} \\ $$$${simple}\:{solution}! \\ $$
