Question Number 118990 by Algoritm last updated on 21/Oct/20
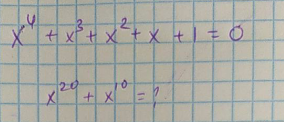
Answered by mr W last updated on 22/Oct/20
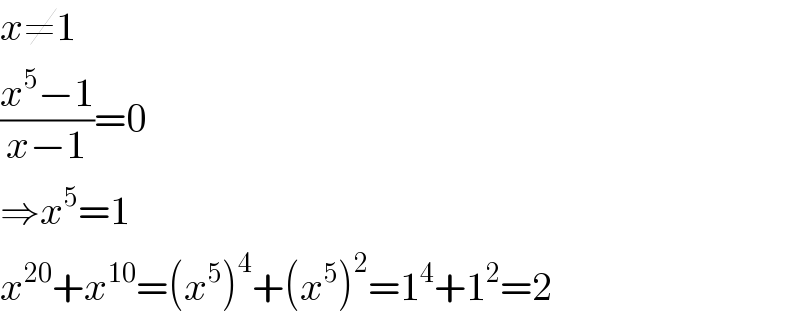
$${x}\neq\mathrm{1} \\ $$$$\frac{{x}^{\mathrm{5}} −\mathrm{1}}{{x}−\mathrm{1}}=\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{5}} =\mathrm{1} \\ $$$${x}^{\mathrm{20}} +{x}^{\mathrm{10}} =\left({x}^{\mathrm{5}} \right)^{\mathrm{4}} +\left({x}^{\mathrm{5}} \right)^{\mathrm{2}} =\mathrm{1}^{\mathrm{4}} +\mathrm{1}^{\mathrm{2}} =\mathrm{2} \\ $$
Answered by Bird last updated on 22/Oct/20
![⇒((1−x^5 )/(1−x))=0 ⇒x^5 =1 and x≠1 the roots of z^(5 ) =1 are z_k =e^((i2kπ)/5) k∈[1,4] z_k ^(20) +z_k ^(10) =e^(8ikπ) +e^(4ikπ) =1+1=2](https://www.tinkutara.com/question/Q119089.png)
$$\Rightarrow\frac{\mathrm{1}−{x}^{\mathrm{5}} }{\mathrm{1}−{x}}=\mathrm{0}\:\Rightarrow{x}^{\mathrm{5}} =\mathrm{1}\:{and}\:{x}\neq\mathrm{1} \\ $$$${the}\:{roots}\:{of}\:{z}^{\mathrm{5}\:} \:=\mathrm{1}\:{are}\:{z}_{{k}} ={e}^{\frac{{i}\mathrm{2}{k}\pi}{\mathrm{5}}} \\ $$$${k}\in\left[\mathrm{1},\mathrm{4}\right] \\ $$$${z}_{{k}} ^{\mathrm{20}} \:+{z}_{{k}} ^{\mathrm{10}} \:={e}^{\mathrm{8}{ik}\pi} \:+{e}^{\mathrm{4}{ik}\pi} \:=\mathrm{1}+\mathrm{1}=\mathrm{2} \\ $$
