Question Number 120823 by bramlexs22 last updated on 03/Nov/20
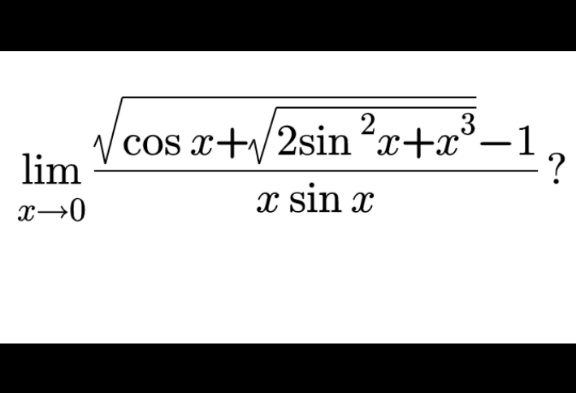
Answered by liberty last updated on 03/Nov/20
![ρ = lim_(x→0) (((√(cos x+(√(2sin^2 x+x^3 ))))−1)/(xsin x)) ρ= lim_(x→0) (((cos x−1)+(√(2sin^2 x+x^3 )))/(x sin x)) .((1/2)) ρ=(1/2) [lim_(x→0) ((−2sin^2 (x/2))/(x sin x)) + lim_(x→0) (√((2sin^2 x+x^3 )/(x^2 sin^2 x))) ] the second limit lim_(x→0) (√((2sin^2 x+x^3 )/(x^2 sin^2 x))) = lim_(x→0) (√((x^2 (2+x))/(x^2 .x^2 ))) = lim_(x→0) (√((2+x)/x^2 )) = ∞ [ as x→0 ∧ sin x ≈ x ]](https://www.tinkutara.com/question/Q120824.png)
$$\:\rho\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\sqrt{\mathrm{cos}\:\mathrm{x}+\sqrt{\mathrm{2sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{x}^{\mathrm{3}} }}−\mathrm{1}}{\mathrm{xsin}\:\mathrm{x}} \\ $$$$\:\rho=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{cos}\:\mathrm{x}−\mathrm{1}\right)+\sqrt{\mathrm{2sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{x}^{\mathrm{3}} }}{\mathrm{x}\:\mathrm{sin}\:\mathrm{x}}\:.\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:\rho=\frac{\mathrm{1}}{\mathrm{2}}\:\left[\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{2sin}\:^{\mathrm{2}} \left(\mathrm{x}/\mathrm{2}\right)}{\mathrm{x}\:\mathrm{sin}\:\mathrm{x}}\:+\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\sqrt{\frac{\mathrm{2sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{x}^{\mathrm{3}} }{\mathrm{x}^{\mathrm{2}} \:\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}}\:\right] \\ $$$$\mathrm{the}\:\mathrm{second}\:\mathrm{limit}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\sqrt{\frac{\mathrm{2sin}\:^{\mathrm{2}} \mathrm{x}+\mathrm{x}^{\mathrm{3}} }{\mathrm{x}^{\mathrm{2}} \:\mathrm{sin}\:^{\mathrm{2}} \mathrm{x}}}\:=\: \\ $$$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\sqrt{\frac{\mathrm{x}^{\mathrm{2}} \left(\mathrm{2}+\mathrm{x}\right)}{\mathrm{x}^{\mathrm{2}} .\mathrm{x}^{\mathrm{2}} }}\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\sqrt{\frac{\mathrm{2}+\mathrm{x}}{\mathrm{x}^{\mathrm{2}} }}\:=\:\infty\: \\ $$$$\left[\:\mathrm{as}\:\mathrm{x}\rightarrow\mathrm{0}\:\wedge\:\mathrm{sin}\:\mathrm{x}\:\approx\:\mathrm{x}\:\right]\: \\ $$
