Question Number 121693 by mathace last updated on 11/Nov/20

Commented by prakash jain last updated on 12/Nov/20
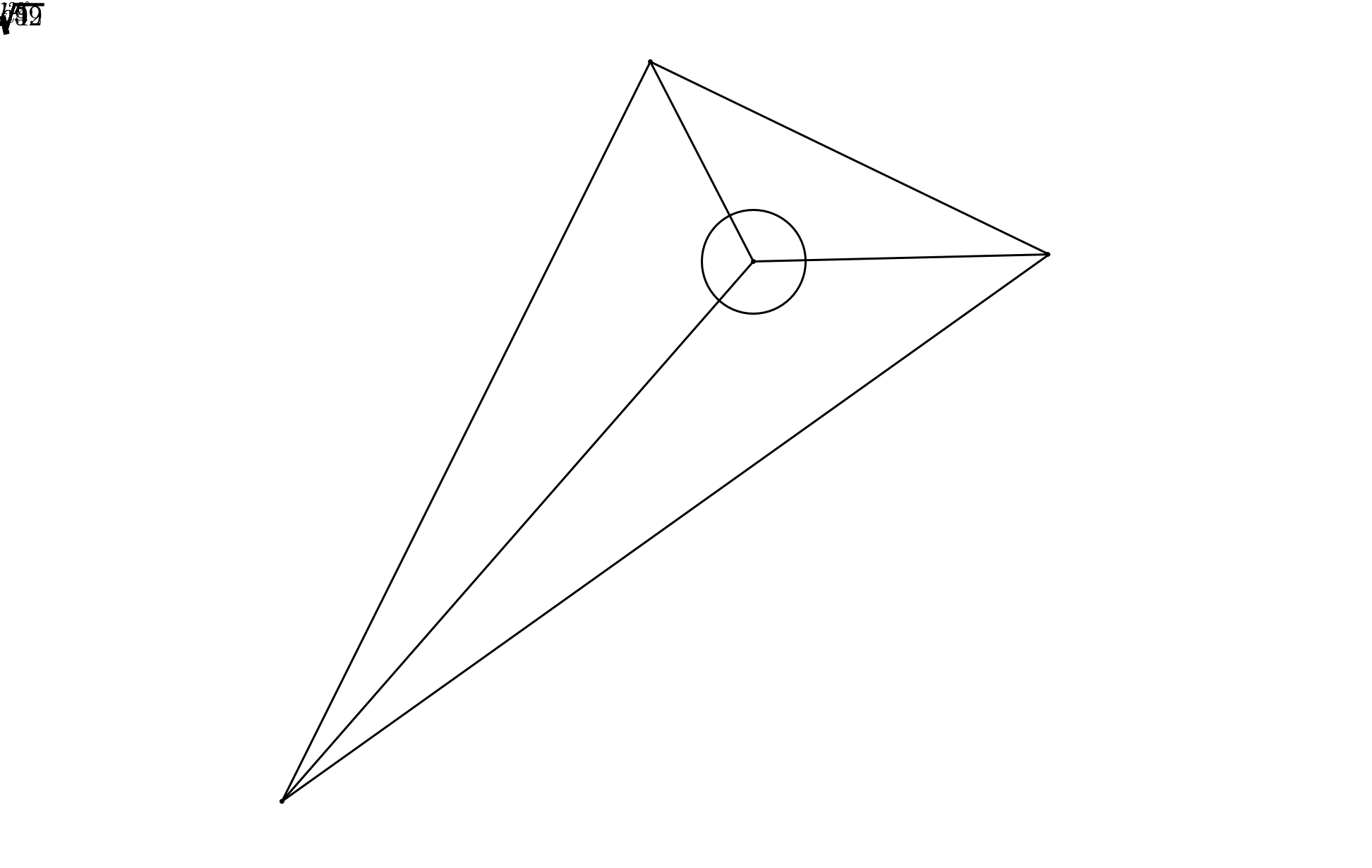
$$ \\ $$
Commented by mindispower last updated on 11/Nov/20

$${nice}\:{sir} \\ $$
Answered by mindispower last updated on 11/Nov/20
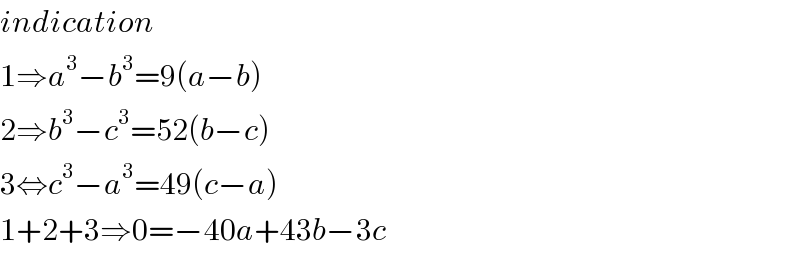
$${indication} \\ $$$$\mathrm{1}\Rightarrow{a}^{\mathrm{3}} −{b}^{\mathrm{3}} =\mathrm{9}\left({a}−{b}\right) \\ $$$$\mathrm{2}\Rightarrow{b}^{\mathrm{3}} −{c}^{\mathrm{3}} =\mathrm{52}\left({b}−{c}\right) \\ $$$$\mathrm{3}\Leftrightarrow{c}^{\mathrm{3}} −{a}^{\mathrm{3}} =\mathrm{49}\left({c}−{a}\right) \\ $$$$\mathrm{1}+\mathrm{2}+\mathrm{3}\Rightarrow\mathrm{0}=−\mathrm{40}{a}+\mathrm{43}{b}−\mathrm{3}{c} \\ $$
Answered by mathace last updated on 12/Nov/20
![The system of equation is a^2 +ab+b^2 =9 (1) b^2 +bc+c^2 =52 (2) c^2 +ac+a^2 =49 (3) The system implies to a^2 +b^2 −((√9))^2 =−ab as a triangle where ((a^2 +b^2 −((√9))^2 )/(2ab))=−(1/2)=cos (120°) (4) similarly, ((b^2 +c^2 −((√(52)))^2 )/(2bc)) =−(1/2)=cos (120°) (5) ((c^2 +a^2 −((√(49)))^2 )/(2ca))=−(1/2)=cos (120°) (6) sum of area of three triangles △OAB,△OBC,△OCA is (1/2)(ab+bc+ca)sin (120°) From the whole triangle △ABC we have, cos (θ)=((7^2 +3^2 −((√(52)))^2 )/(2×7×3))=(1/7) implies, sin (θ)=±((√(48))/7) (7) Considering the positve value of sin (θ) we find the area of the whole triangle △ABC is (1/2)×7×3×sin (θ)=(1/2)×7×3×((√(48))/7)=(3/2)(√(48)) As sum of tringles △OAB, △OBC, △OCA is equal to the area of the whole triangle△ABC, thus we have (1/2)(ab+bc+ca)sin (120°)=(3/2)(√(48)) or, ab+bc+ca=24 Now, (1)+(2)+(3) implies 2(a^2 +b^2 +c^2 )+(ab+bc+ca)=9+52+49=110 2(a^2 +b^2 +c^2 )=110−24=86 a^2 +b^2 +c^2 =43 We know, (a+b+c)^2 =(a^2 +b^2 +c^2 )+2(ab+bc+ca) (a+b+c)^2 =43+48=91 a+b+c=±(√(91)) Now Applying the oprations (2)−(1), (2)−(3) and (3)−(1) we have, (c−a)(a+b+c)=43 (8) (b−a)(a+b+c)=3 (9) (c−b)(a+b+c)=40 (10) Hence, our quadratic system has been transformed into equivalent linear system. Thus we have, c−a=±((43)/( (√(91)))) b−a=±(3/( (√(91)))) c−b=±((40)/( (√(91)))) a+b+c=±(√(91)) Solving the system we have, a=±((15)/( (√(91)))) b=±((18)/( (√(91)))) c=±((58)/( (√(91)))) Again from equation (7), we have sin (θ)=−((√(48))/7) [Taking(−ve)value] Now the area of the whole triangle △ABC is (1/2)×7×3×sin (θ)=(1/2)×7×3×(−((√(48))/7))=−(3/2)(√(48)) As sum of tringles △OAB, △OBC, △OCA is equal to the area of the whole triangle△ABC, thus we have (1/2)(ab+bc+ca)sin (120°)=−(3/2)(√(48)) or, ab+bc+ca=−24 Now, (1)+(2)+(3) implies 2(a^2 +b^2 +c^2 )+(ab+bc+ca)=9+52+49=110 2(a^2 +b^2 +c^2 )=110+24=134 a^2 +b^2 +c^2 =67 We know, (a+b+c)^2 =(a^2 +b^2 +c^2 )+2(ab+bc+ca) (a+b+c)^2 =67−48=19 a+b+c=±(√(19)) Now recalling the equation (8),(9),(10) we have (c−a)(a+b+c)=43 (b−a)(a+b+c)=3 (c−b)(a+b+c)=40 Hence, our quadratic system has been transformed again into equivalent linear system. Thus we have, c−a=±((43)/( (√(19)))) b−a=±(3/( (√(19)))) c−b=±((40)/( (√(19)))) a+b+c=±(√(19)) Solving the system we have, a=∓(9/( (√(19)))) b=∓(6/( (√(19)))) c=±((34)/( (√(19)))) Therefore our obtained solution set S={(a,b,c):(((15)/( (√(91)))),((18)/( (√(91)))),((58)/( (√(91))))),(((−15)/( (√(91)))),((−18)/( (√(91)))),((−58)/( (√(91))))),(((−9)/( (√(19)))),((−6)/( (√(19)))),((34)/( (√(19))))),((9/( (√(19)))),(6/( (√(19)))),((−34)/( (√(19)))))} [Omar bin Abdul Aziz]](https://www.tinkutara.com/question/Q121828.png)
$$ \\ $$$${The}\:{system}\:{of}\:{equation}\:{is} \\ $$$${a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} =\mathrm{9}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$${b}^{\mathrm{2}} +{bc}+{c}^{\mathrm{2}} =\mathrm{52}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$${c}^{\mathrm{2}} +{ac}+{a}^{\mathrm{2}} =\mathrm{49}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{3}\right) \\ $$$${The}\:{system}\:{implies}\:{to} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\left(\sqrt{\mathrm{9}}\right)^{\mathrm{2}} =−{ab}\:\:\:\:\:\:{as}\:{a}\:{triangle}\:{where} \\ $$$$\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\left(\sqrt{\mathrm{9}}\right)^{\mathrm{2}} }{\mathrm{2}{ab}}=−\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{cos}\:\left(\mathrm{120}°\right)\:\:\:\:\:\:\:\:\left(\mathrm{4}\right) \\ $$$${similarly}, \\ $$$$\frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\left(\sqrt{\mathrm{52}}\right)^{\mathrm{2}} }{\mathrm{2}{bc}}\:=−\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{cos}\:\left(\mathrm{120}°\right)\:\:\:\:\:\left(\mathrm{5}\right) \\ $$$$\frac{{c}^{\mathrm{2}} +{a}^{\mathrm{2}} −\left(\sqrt{\mathrm{49}}\right)^{\mathrm{2}} }{\mathrm{2}{ca}}=−\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{cos}\:\left(\mathrm{120}°\right)\:\:\:\:\:\:\left(\mathrm{6}\right) \\ $$$$ \\ $$$${sum}\:{of}\:{area}\:{of}\:{three}\:{triangles}\:\:\bigtriangleup{OAB},\bigtriangleup{OBC},\bigtriangleup{OCA}\:{is} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left({ab}+{bc}+{ca}\right)\mathrm{sin}\:\left(\mathrm{120}°\right) \\ $$$${From}\:{the}\:{whole}\:{triangle}\:\bigtriangleup{ABC}\:{we}\:{have}, \\ $$$$\mathrm{cos}\:\left(\theta\right)=\frac{\mathrm{7}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} −\left(\sqrt{\mathrm{52}}\right)^{\mathrm{2}} }{\mathrm{2}×\mathrm{7}×\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{7}} \\ $$$${implies},\:\:\mathrm{sin}\:\left(\theta\right)=\pm\frac{\sqrt{\mathrm{48}}}{\mathrm{7}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{7}\right) \\ $$$${Considering}\:{the}\:{positve}\:{value}\:{of}\:\mathrm{sin}\:\left(\theta\right)\:{we}\:{find} \\ $$$${the}\:{area}\:{of}\:{the}\:{whole}\:{triangle}\:\bigtriangleup{ABC}\:\:{is} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{7}×\mathrm{3}×\mathrm{sin}\:\left(\theta\right)=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{7}×\mathrm{3}×\frac{\sqrt{\mathrm{48}}}{\mathrm{7}}=\frac{\mathrm{3}}{\mathrm{2}}\sqrt{\mathrm{48}} \\ $$$${As}\:{sum}\:{of}\:{tringles}\:\bigtriangleup{OAB},\:\bigtriangleup{OBC},\:\bigtriangleup{OCA}\:{is}\:{equal}\:{to}\:{the} \\ $$$${area}\:{of}\:{the}\:{whole}\:{triangle}\bigtriangleup{ABC},\:{thus}\:{we}\:{have} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left({ab}+{bc}+{ca}\right)\mathrm{sin}\:\left(\mathrm{120}°\right)=\frac{\mathrm{3}}{\mathrm{2}}\sqrt{\mathrm{48}}\:\:{or}, \\ $$$${ab}+{bc}+{ca}=\mathrm{24} \\ $$$${Now},\:\left(\mathrm{1}\right)+\left(\mathrm{2}\right)+\left(\mathrm{3}\right)\:{implies} \\ $$$$\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)+\left({ab}+{bc}+{ca}\right)=\mathrm{9}+\mathrm{52}+\mathrm{49}=\mathrm{110} \\ $$$$\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)=\mathrm{110}−\mathrm{24}=\mathrm{86} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{43} \\ $$$${We}\:{know}, \\ $$$$\left({a}+{b}+{c}\right)^{\mathrm{2}} =\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)+\mathrm{2}\left({ab}+{bc}+{ca}\right) \\ $$$$\left({a}+{b}+{c}\right)^{\mathrm{2}} =\mathrm{43}+\mathrm{48}=\mathrm{91} \\ $$$${a}+{b}+{c}=\pm\sqrt{\mathrm{91}} \\ $$$${Now}\:{Applying}\:{the}\:{oprations}\:\:\left(\mathrm{2}\right)−\left(\mathrm{1}\right), \\ $$$$\left(\mathrm{2}\right)−\left(\mathrm{3}\right)\:{and}\:\left(\mathrm{3}\right)−\left(\mathrm{1}\right)\:{we}\:{have}, \\ $$$$\left({c}−{a}\right)\left({a}+{b}+{c}\right)=\mathrm{43}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{8}\right) \\ $$$$\left({b}−{a}\right)\left({a}+{b}+{c}\right)=\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{9}\right) \\ $$$$\left({c}−{b}\right)\left({a}+{b}+{c}\right)=\mathrm{40}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{10}\right) \\ $$$${Hence},\:{our}\:{quadratic}\:{system}\:{has}\:{been}\: \\ $$$${transformed}\:{into}\:{equivalent}\:{linear}\:{system}. \\ $$$${Thus}\:{we}\:{have}, \\ $$$${c}−{a}=\pm\frac{\mathrm{43}}{\:\sqrt{\mathrm{91}}} \\ $$$${b}−{a}=\pm\frac{\mathrm{3}}{\:\sqrt{\mathrm{91}}} \\ $$$${c}−{b}=\pm\frac{\mathrm{40}}{\:\sqrt{\mathrm{91}}} \\ $$$${a}+{b}+{c}=\pm\sqrt{\mathrm{91}} \\ $$$${Solving}\:{the}\:{system}\:{we}\:{have}, \\ $$$${a}=\pm\frac{\mathrm{15}}{\:\sqrt{\mathrm{91}}} \\ $$$${b}=\pm\frac{\mathrm{18}}{\:\sqrt{\mathrm{91}}} \\ $$$${c}=\pm\frac{\mathrm{58}}{\:\sqrt{\mathrm{91}}} \\ $$$${Again}\:{from}\:{equation}\:\left(\mathrm{7}\right),\:{we}\:{have} \\ $$$$\:\mathrm{sin}\:\left(\theta\right)=−\frac{\sqrt{\mathrm{48}}}{\mathrm{7}}\:\left[{Taking}\left(−{ve}\right){value}\right]\: \\ $$$${Now}\:{the}\:{area}\:{of}\:{the}\:{whole}\:{triangle}\:\bigtriangleup{ABC}\:\:{is} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{7}×\mathrm{3}×\mathrm{sin}\:\left(\theta\right)=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{7}×\mathrm{3}×\left(−\frac{\sqrt{\mathrm{48}}}{\mathrm{7}}\right)=−\frac{\mathrm{3}}{\mathrm{2}}\sqrt{\mathrm{48}} \\ $$$${As}\:{sum}\:{of}\:{tringles}\:\bigtriangleup{OAB},\:\bigtriangleup{OBC},\:\bigtriangleup{OCA}\:{is}\:{equal}\:{to}\:{the} \\ $$$${area}\:{of}\:{the}\:{whole}\:{triangle}\bigtriangleup{ABC},\:{thus}\:{we}\:{have} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left({ab}+{bc}+{ca}\right)\mathrm{sin}\:\left(\mathrm{120}°\right)=−\frac{\mathrm{3}}{\mathrm{2}}\sqrt{\mathrm{48}}\:\:{or}, \\ $$$${ab}+{bc}+{ca}=−\mathrm{24} \\ $$$${Now},\:\left(\mathrm{1}\right)+\left(\mathrm{2}\right)+\left(\mathrm{3}\right)\:{implies} \\ $$$$\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)+\left({ab}+{bc}+{ca}\right)=\mathrm{9}+\mathrm{52}+\mathrm{49}=\mathrm{110} \\ $$$$\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)=\mathrm{110}+\mathrm{24}=\mathrm{134} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} =\mathrm{67} \\ $$$${We}\:{know}, \\ $$$$\left({a}+{b}+{c}\right)^{\mathrm{2}} =\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)+\mathrm{2}\left({ab}+{bc}+{ca}\right) \\ $$$$\left({a}+{b}+{c}\right)^{\mathrm{2}} =\mathrm{67}−\mathrm{48}=\mathrm{19} \\ $$$${a}+{b}+{c}=\pm\sqrt{\mathrm{19}} \\ $$$${Now}\:{recalling}\:{the}\:{equation}\:\left(\mathrm{8}\right),\left(\mathrm{9}\right),\left(\mathrm{10}\right)\:{we}\:{have} \\ $$$$\left({c}−{a}\right)\left({a}+{b}+{c}\right)=\mathrm{43} \\ $$$$\left({b}−{a}\right)\left({a}+{b}+{c}\right)=\mathrm{3} \\ $$$$\left({c}−{b}\right)\left({a}+{b}+{c}\right)=\mathrm{40} \\ $$$${Hence},\:{our}\:{quadratic}\:{system}\:{has}\:{been}\: \\ $$$${transformed}\:{again}\:{into}\:{equivalent}\:{linear}\:{system}. \\ $$$${Thus}\:{we}\:{have}, \\ $$$${c}−{a}=\pm\frac{\mathrm{43}}{\:\sqrt{\mathrm{19}}} \\ $$$${b}−{a}=\pm\frac{\mathrm{3}}{\:\sqrt{\mathrm{19}}} \\ $$$${c}−{b}=\pm\frac{\mathrm{40}}{\:\sqrt{\mathrm{19}}} \\ $$$${a}+{b}+{c}=\pm\sqrt{\mathrm{19}} \\ $$$${Solving}\:{the}\:{system}\:{we}\:{have}, \\ $$$${a}=\mp\frac{\mathrm{9}}{\:\sqrt{\mathrm{19}}} \\ $$$${b}=\mp\frac{\mathrm{6}}{\:\sqrt{\mathrm{19}}} \\ $$$${c}=\pm\frac{\mathrm{34}}{\:\sqrt{\mathrm{19}}} \\ $$$$\:{Therefore}\:{our}\:{obtained}\:{solution}\:{set}\: \\ $$$${S}=\left\{\left({a},{b},{c}\right):\left(\frac{\mathrm{15}}{\:\sqrt{\mathrm{91}}},\frac{\mathrm{18}}{\:\sqrt{\mathrm{91}}},\frac{\mathrm{58}}{\:\sqrt{\mathrm{91}}}\right),\left(\frac{−\mathrm{15}}{\:\sqrt{\mathrm{91}}},\frac{−\mathrm{18}}{\:\sqrt{\mathrm{91}}},\frac{−\mathrm{58}}{\:\sqrt{\mathrm{91}}}\right),\left(\frac{−\mathrm{9}}{\:\sqrt{\mathrm{19}}},\frac{−\mathrm{6}}{\:\sqrt{\mathrm{19}}},\frac{\mathrm{34}}{\:\sqrt{\mathrm{19}}}\right),\left(\frac{\mathrm{9}}{\:\sqrt{\mathrm{19}}},\frac{\mathrm{6}}{\:\sqrt{\mathrm{19}}},\frac{−\mathrm{34}}{\:\sqrt{\mathrm{19}}}\right)\right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left[{Omar}\:{bin}\:{Abdul}\:{Aziz}\right] \\ $$
