Question Number 122822 by bemath last updated on 19/Nov/20
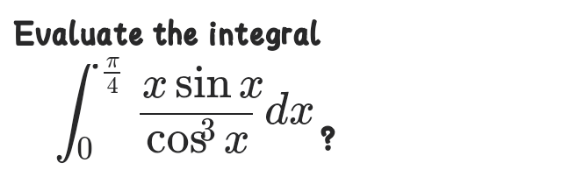
Answered by liberty last updated on 20/Nov/20
![I=∫ x tan x sec^2 x dx = ∫ x tan x d(tan x) by D.I method → { ((u=x→du=dx)),((v=∫tan x d(tan x)=(1/2)tan^2 x)) :} I=(1/2)x.tan^2 x−(1/2)∫tan^2 x dx I=(1/2)x.tan^2 x−(1/2)∫ (sec^2 x−1)dx I=(1/2)x.tan^2 x−(1/2)tan x+(1/2)x+c thus ∫_0 ^(π/4) ((x.sin x)/(cos^3 x)) dx = [ (1/2)x.tan^2 x−(1/2)tan x+(1/2)x+c ]_0 ^(π/4) = ((2π)/8)−(1/2)= ((π−2)/4).▲](https://www.tinkutara.com/question/Q122827.png)
$${I}=\int\:{x}\:\mathrm{tan}\:{x}\:\mathrm{sec}\:^{\mathrm{2}} {x}\:{dx}\:=\:\int\:{x}\:\mathrm{tan}\:{x}\:{d}\left(\mathrm{tan}\:{x}\right) \\ $$$${by}\:{D}.{I}\:{method}\:\rightarrow\begin{cases}{{u}={x}\rightarrow{du}={dx}}\\{{v}=\int\mathrm{tan}\:{x}\:{d}\left(\mathrm{tan}\:{x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}\:^{\mathrm{2}} {x}}\end{cases} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}{x}.\mathrm{tan}\:^{\mathrm{2}} {x}−\frac{\mathrm{1}}{\mathrm{2}}\int\mathrm{tan}\:^{\mathrm{2}} {x}\:{dx}\: \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}{x}.\mathrm{tan}\:^{\mathrm{2}} {x}−\frac{\mathrm{1}}{\mathrm{2}}\int\:\left(\mathrm{sec}\:^{\mathrm{2}} {x}−\mathrm{1}\right){dx} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}{x}.\mathrm{tan}\:^{\mathrm{2}} {x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}\:{x}+\frac{\mathrm{1}}{\mathrm{2}}{x}+{c} \\ $$$${thus}\:\underset{\mathrm{0}} {\overset{\pi/\mathrm{4}} {\int}}\frac{{x}.\mathrm{sin}\:{x}}{\mathrm{cos}\:^{\mathrm{3}} {x}}\:{dx}\:=\:\left[\:\frac{\mathrm{1}}{\mathrm{2}}{x}.\mathrm{tan}\:^{\mathrm{2}} {x}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{tan}\:{x}+\frac{\mathrm{1}}{\mathrm{2}}{x}+{c}\:\right]_{\mathrm{0}} ^{\pi/\mathrm{4}} \\ $$$$\:\:=\:\frac{\mathrm{2}\pi}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{2}}=\:\frac{\pi−\mathrm{2}}{\mathrm{4}}.\blacktriangle \\ $$
