Question Number 126607 by shaker last updated on 22/Dec/20
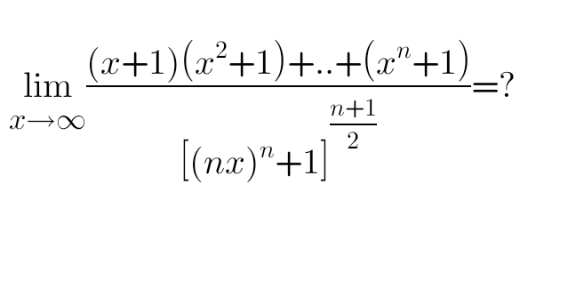
Answered by Olaf last updated on 22/Dec/20
![∼_∞ (x^(1+2+3+...+n) /([(nx)^n ]^((n+1)/2) )) = (x^((n(n+1))/2) /(n^((n(n+1))/2) x^((n(n+1))/2) )) = (1/n^((n(n+1))/2) )](https://www.tinkutara.com/question/Q126625.png)
$$\underset{\infty} {\sim}\:\frac{{x}^{\mathrm{1}+\mathrm{2}+\mathrm{3}+…+{n}} }{\left[\left({nx}\right)^{{n}} \right]^{\frac{{n}+\mathrm{1}}{\mathrm{2}}} }\:=\:\frac{{x}^{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}} }{{n}^{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}} {x}^{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}} }\:=\:\frac{\mathrm{1}}{{n}^{\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}}} } \\ $$
