Question Number 13029 by chux last updated on 11/May/17
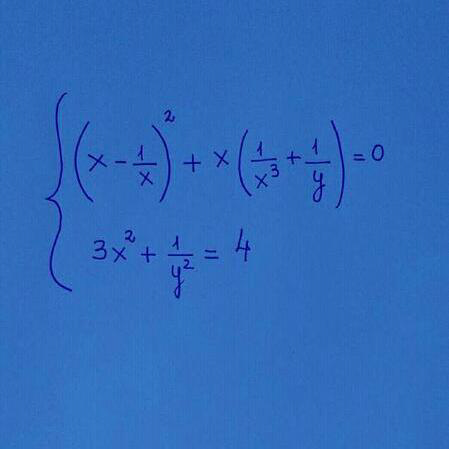
Commented by chux last updated on 12/May/17
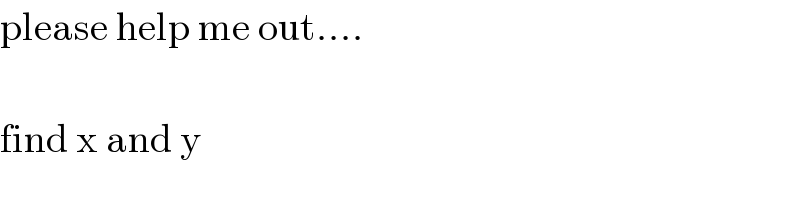
$$\mathrm{please}\:\mathrm{help}\:\mathrm{me}\:\mathrm{out}….\: \\ $$$$ \\ $$$$\mathrm{find}\:\mathrm{x}\:\mathrm{and}\:\mathrm{y} \\ $$
Answered by ajfour last updated on 12/May/17
![(x−(1/x))^2 +(1/x^2 )+(x/y)=0 .....(1) or [(x−(1/x))^2 +(1/x^2 )]^2 =(x^2 /y^2 ) ....(i) further 3x^2 +(1/y^2 )=4 ......(2) ⇒ 3x^4 +(x^2 /y^2 )=4x^2 ......(ii) so [(x−(1/x))^2 +(1/x^2 )]^2 =4x^2 −3x^4 (x^2 −2+(2/x^2 ))^2 =4x^2 −3x^4 x^4 +4+(4/x^4 )+2(−2x^2 +2−(4/x^2 ))=4x^2 −3x^4 x^4 +4+(4/x^4 )−4x^2 +4−(8/x^2 )=4x^2 −3x^4 4x^4 +8+(4/x^4 )−8x^2 −(8/x^2 )=0 4(x^2 +(1/x^2 ))^2 =8(x^2 +(1/x^2 )) ⇒x^2 +(1/x^2 )=2 x^2 −2+(1/x^2 ) =0 (x−(1/x))^2 =0 x=(1/x) ⇒ x^2 =1 x=±1 substituting for x in equation ..(1) which becomes y=−x^3 , as (x−(1/x))=0 so y=∓1 solution is (1, −1) and (−1, 1) .](https://www.tinkutara.com/question/Q13052.png)
$$\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{{x}}{{y}}=\mathrm{0}\:\:…..\left(\mathrm{1}\right) \\ $$$${or}\:\left[\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right]^{\mathrm{2}} =\frac{{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} }\:\:….\left({i}\right) \\ $$$${further}\:\:\:\:\:\mathrm{3}{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{y}^{\mathrm{2}} }=\mathrm{4}\:\:\:\:……\left(\mathrm{2}\right) \\ $$$$\Rightarrow\:\mathrm{3}{x}^{\mathrm{4}} +\frac{{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} }=\mathrm{4}{x}^{\mathrm{2}} \:\:\:\:……\left({ii}\right) \\ $$$${so}\:\:\left[\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right]^{\mathrm{2}} =\mathrm{4}{x}^{\mathrm{2}} −\mathrm{3}{x}^{\mathrm{4}} \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{2}+\frac{\mathrm{2}}{{x}^{\mathrm{2}} }\right)^{\mathrm{2}} =\mathrm{4}{x}^{\mathrm{2}} −\mathrm{3}{x}^{\mathrm{4}} \\ $$$${x}^{\mathrm{4}} +\mathrm{4}+\frac{\mathrm{4}}{{x}^{\mathrm{4}} }+\mathrm{2}\left(−\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}−\frac{\mathrm{4}}{{x}^{\mathrm{2}} }\right)=\mathrm{4}{x}^{\mathrm{2}} −\mathrm{3}{x}^{\mathrm{4}} \\ $$$${x}^{\mathrm{4}} +\mathrm{4}+\frac{\mathrm{4}}{{x}^{\mathrm{4}} }−\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}−\frac{\mathrm{8}}{{x}^{\mathrm{2}} }=\mathrm{4}{x}^{\mathrm{2}} −\mathrm{3}{x}^{\mathrm{4}} \\ $$$$\mathrm{4}{x}^{\mathrm{4}} +\mathrm{8}+\frac{\mathrm{4}}{{x}^{\mathrm{4}} }−\mathrm{8}{x}^{\mathrm{2}} −\frac{\mathrm{8}}{{x}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\mathrm{4}\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\mathrm{2}} =\mathrm{8}\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right) \\ $$$$\Rightarrow{x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }=\mathrm{2} \\ $$$${x}^{\mathrm{2}} −\mathrm{2}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:=\mathrm{0} \\ $$$$\left({x}−\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$${x}=\frac{\mathrm{1}}{{x}}\:\:\:\:\:\Rightarrow\:\:\:{x}^{\mathrm{2}} =\mathrm{1} \\ $$$${x}=\pm\mathrm{1}\: \\ $$$${substituting}\:{for}\:{x}\:{in}\:{equation}\:..\left(\mathrm{1}\right) \\ $$$${which}\:{becomes}\:\:{y}=−{x}^{\mathrm{3}} \:,\:{as}\:\left({x}−\frac{\mathrm{1}}{{x}}\right)=\mathrm{0} \\ $$$${so}\:\:\:{y}=\mp\mathrm{1} \\ $$$${solution}\:{is}\:\left(\mathrm{1},\:−\mathrm{1}\right)\:\:{and}\:\:\left(−\mathrm{1},\:\mathrm{1}\right)\:. \\ $$
Commented by chux last updated on 13/May/17

$$\mathrm{this}\:\mathrm{is}\:\mathrm{wonderful} \\ $$
Commented by RasheedSindhi last updated on 12/May/17

$$\Sigma\mathrm{xcelent}! \\ $$
Commented by ajfour last updated on 12/May/17

$${thanks}. \\ $$
Commented by mrW1 last updated on 13/May/17

$${great}! \\ $$
