Question Number 147746 by 0731619 last updated on 23/Jul/21
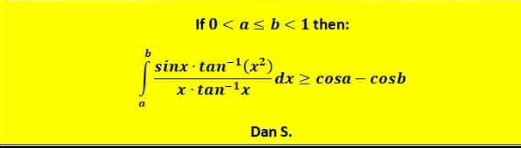
Answered by mindispower last updated on 23/Jul/21
![((tan^− (x^2 ))/(tan^− (x)))<1 x≤x^2 <1, and using tan^− increasing function ∀x∈]a,b[ x<1⇒xsin(x)<sin(x) ⇒((sin(x))/x)>sin(x) ⇒((sin(x))/x).((tan^− (x^2 ))/(tan^− (x)))dx>sin(x) ∫_a ^b ((sin(x)tan^− (x^2 ))/(x.tan^− (x)))dx>∫_a ^b sin(x)dx=cos(a)−cos(b)](https://www.tinkutara.com/question/Q147765.png)
$$\frac{{tan}^{−} \left({x}^{\mathrm{2}} \right)}{{tan}^{−} \left({x}\right)}<\mathrm{1} \\ $$$${x}\leqslant{x}^{\mathrm{2}} <\mathrm{1},\:{and}\:{using}\:{tan}^{−} \:{increasing}\:{function} \\ $$$$\left.\forall{x}\in\right]{a},{b}\left[\:{x}<\mathrm{1}\Rightarrow{xsin}\left({x}\right)<{sin}\left({x}\right)\right. \\ $$$$\Rightarrow\frac{{sin}\left({x}\right)}{{x}}>{sin}\left({x}\right) \\ $$$$\Rightarrow\frac{{sin}\left({x}\right)}{{x}}.\frac{{ta}\overset{−} {{n}}\left({x}^{\mathrm{2}} \right)}{{tan}^{−} \left(\boldsymbol{{x}}\right)}\boldsymbol{{dx}}>\boldsymbol{{sin}}\left(\boldsymbol{{x}}\right) \\ $$$$\int_{{a}} ^{{b}} \frac{{sin}\left({x}\right){tan}^{−} \left({x}^{\mathrm{2}} \right)}{{x}.{tan}^{−} \left({x}\right)}{dx}>\int_{{a}} ^{{b}} {sin}\left({x}\right){dx}={cos}\left({a}\right)−{cos}\left({b}\right) \\ $$
