Question-150033

Question Number 150033 by cherokeesay last updated on 08/Aug/21

Answered by maged last updated on 09/Aug/21

A_c =((πR^2 )/2)=((36π)/2)=18π ∣BH∣=Rsin 60°=6×((√3)/2)=3(√3) A_y =A_s +A_t =∣BH∣^2 +((∣BH∣)/2)×(R/2)=27+((3(√3))/2)×3=9(3+((√3)/2)) A_x =A_c −A_y A_x =18π−9((6+(√3))/2)=18(π−((6+(√3))/4))=9(((4π−6−(√3))/2)) (A_x /A_c )=((9(((4π−6−(√3))/2)))/(18π))=((4π−6−(√3))/(4π))=[1−(√3)(((3(√3)+1)/(4π)))]%

$${A}_{{c}} =\frac{\pi{R}^{\mathrm{2}} }{\mathrm{2}}=\frac{\mathrm{36}\pi}{\mathrm{2}}=\mathrm{18}\pi \\ $$$$\mid{BH}\mid={R}\mathrm{sin}\:\mathrm{60}°=\mathrm{6}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}=\mathrm{3}\sqrt{\mathrm{3}} \\ $$$${A}_{{y}} ={A}_{{s}} +{A}_{{t}} =\mid{BH}\mid^{\mathrm{2}} +\frac{\mid{BH}\mid}{\mathrm{2}}×\frac{{R}}{\mathrm{2}}=\mathrm{27}+\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}×\mathrm{3}=\mathrm{9}\left(\mathrm{3}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$${A}_{{x}} ={A}_{{c}} −{A}_{{y}} \\ $$$${A}_{{x}} =\mathrm{18}\pi−\mathrm{9}\frac{\mathrm{6}+\sqrt{\mathrm{3}}}{\mathrm{2}}=\mathrm{18}\left(\pi−\frac{\mathrm{6}+\sqrt{\mathrm{3}}}{\mathrm{4}}\right)=\mathrm{9}\left(\frac{\mathrm{4}\pi−\mathrm{6}−\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$$\frac{{A}_{{x}} }{{A}_{{c}} }=\frac{\mathrm{9}\left(\frac{\mathrm{4}\pi−\mathrm{6}−\sqrt{\mathrm{3}}}{\mathrm{2}}\right)}{\mathrm{18}\pi}=\frac{\mathrm{4}\pi−\mathrm{6}−\sqrt{\mathrm{3}}}{\mathrm{4}\pi}=\left[\mathrm{1}−\sqrt{\mathrm{3}}\left(\frac{\mathrm{3}\sqrt{\mathrm{3}}+\mathrm{1}}{\mathrm{4}\pi}\right)\right]\% \\ $$

Commented by cherokeesay last updated on 09/Aug/21

$${ABDH}\:{is}\:{not}\:{a}\:{square}\:! \\ $$

Commented by cherokeesay last updated on 09/Aug/21

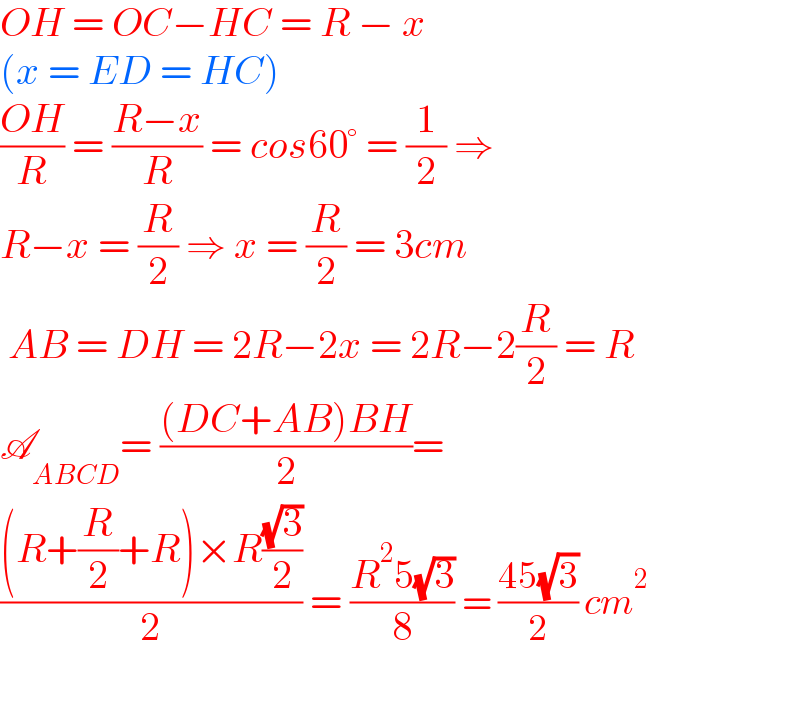
OH = OC−HC = R − x (x = ED = HC) ((OH)/R) = ((R−x)/R) = cos60° = (1/2) ⇒ R−x = (R/2) ⇒ x = (R/2) = 3cm AB = DH = 2R−2x = 2R−2(R/2) = R A_(ABCD) = (((DC+AB)BH)/2)= (((R+(R/2)+R)×R((√3)/2))/2) = ((R^2 5(√3))/8) = ((45(√3))/2) cm^2

$${OH}\:=\:{OC}−{HC}\:=\:{R}\:−\:{x} \\ $$$$\left({x}\:=\:{ED}\:=\:{HC}\right) \\ $$$$\frac{{OH}}{{R}}\:=\:\frac{{R}−{x}}{{R}}\:=\:{cos}\mathrm{60}°\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\: \\ $$$${R}−{x}\:=\:\frac{{R}}{\mathrm{2}}\:\Rightarrow\:{x}\:=\:\frac{{R}}{\mathrm{2}}\:=\:\mathrm{3}{cm} \\ $$$$\:{AB}\:=\:{DH}\:=\:\mathrm{2}{R}−\mathrm{2}{x}\:=\:\mathrm{2}{R}−\mathrm{2}\frac{{R}}{\mathrm{2}}\:=\:{R} \\ $$$$\mathscr{A}_{{ABCD}} =\:\frac{\left({DC}+{AB}\right){BH}}{\mathrm{2}}=\: \\ $$$$\frac{\left({R}+\frac{{R}}{\mathrm{2}}+{R}\right)×{R}\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}{\mathrm{2}}\:=\:\frac{{R}^{\mathrm{2}} \mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{8}}\:=\:\frac{\mathrm{45}\sqrt{\mathrm{3}}}{\mathrm{2}}\:{cm}^{\mathrm{2}} \\ $$$$ \\ $$

Commented by Rasheed.Sindhi last updated on 09/Aug/21

A_(ABCD) = (((DC+AB)BH)/2) Why have you considered ABCD as a trapizoid? It may be quadrilateral. Can you prove it? When ^• AB may not be paralell toDC ^• AD may not be perpendicular to DC (or EC).

$$\mathscr{A}_{{ABCD}} =\:\frac{\left({DC}+{AB}\right){BH}}{\mathrm{2}} \\ $$$${Why}\:{have}\:{you}\:{considered}\:{ABCD} \\ $$$${as}\:{a}\:{trapizoid}?\:{It}\:{may}\:{be}\:{quadrilateral}. \\ $$$${Can}\:{you}\:{prove}\:{it}?\:{When} \\ $$$$\:^{\bullet} {AB}\:{may}\:{not}\:{be}\:{paralell}\:{toDC} \\ $$$$\:^{\bullet} {AD}\:{may}\:{not}\:{be}\:{perpendicular}\:{to} \\ $$$$\:\:\:\:{DC}\:\left({or}\:{EC}\right). \\ $$

Commented by cherokeesay last updated on 09/Aug/21

$${AB}\://\:{DC} \\ $$$${AD}\:\bot\:{DC}\:\bot\:{EC} \\ $$

Commented by Rasheed.Sindhi last updated on 09/Aug/21

{: ((AB // DC)),((AD ⊥ DC ⊥ EC)) }Not mentkoned in the question, these are only your assumptions!! Anyway thanks for your response.

$$\left.\begin{matrix}{{AB}\://\:{DC}}\\{{AD}\:\bot\:{DC}\:\bot\:{EC}}\end{matrix}\right\}\mathcal{N}{ot}\:{mentkoned}\:{in}\:{the}\:{question}, \\ $$$${these}\:{are}\:{only}\:{your}\:{assumptions}!! \\ $$$${Anyway}\:\:{thanks}\:{for}\:{your}\:{response}. \\ $$

Commented by Rasheed.Sindhi last updated on 09/Aug/21

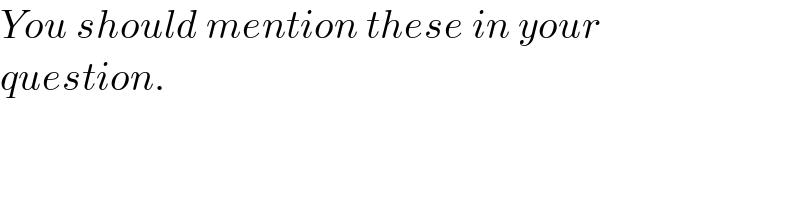
$${You}\:{should}\:{mention}\:{these}\:{in}\:{your} \\ $$$${question}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply