Question Number 150313 by dany last updated on 11/Aug/21

Answered by ajfour last updated on 11/Aug/21
![f(x−y)=f(x)f(y) −f(a−x)f(a+y) y=0 f(x)=f(x)−f(a−x)f(a) ⇒ f(a−x)=0 and/or f(a)=0 x=0 thereafter y=−x f(x)=f(−x)−f(a)f(a−x) ⇒ f(x)=f(−x) f(x) is an even function. x=a, y=x f(a−x)=f(a)f(x)−f(a+x) f(2a−x)=f(a)f(x−a)−f(x) ⇒ f(a−x)+f(a)f(2a−x) = f^2 (a)f(x−a)−f(a+x) f(2a−x)=[f(a)−(1/(f(a)))]f(x−a) −((f(a+x))/(f(a))) x=a, y=0 f(a)=f(a)−f(a)=0 ⇒ f(a−x)=−f(a+x) now x→x−a ⇒ f(2a−x)=−f(x) hence (C).](https://www.tinkutara.com/question/Q150317.png)
$${f}\left({x}−{y}\right)={f}\left({x}\right){f}\left({y}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−{f}\left({a}−{x}\right){f}\left({a}+{y}\right) \\ $$$${y}=\mathrm{0} \\ $$$$\cancel{{f}\left({x}\right)}=\cancel{{f}\left({x}\right)}−{f}\left({a}−{x}\right){f}\left({a}\right) \\ $$$$\Rightarrow\:\:{f}\left({a}−{x}\right)=\mathrm{0}\:\:{and}/{or}\:{f}\left({a}\right)=\mathrm{0} \\ $$$${x}=\mathrm{0}\:{thereafter}\:{y}=−{x} \\ $$$${f}\left({x}\right)={f}\left(−{x}\right)−{f}\left({a}\right){f}\left({a}−{x}\right) \\ $$$$\Rightarrow\:\:{f}\left({x}\right)={f}\left(−{x}\right) \\ $$$${f}\left({x}\right)\:{is}\:{an}\:{even}\:{function}. \\ $$$${x}={a},\:{y}={x} \\ $$$${f}\left({a}−{x}\right)={f}\left({a}\right){f}\left({x}\right)−{f}\left({a}+{x}\right) \\ $$$${f}\left(\mathrm{2}{a}−{x}\right)={f}\left({a}\right){f}\left({x}−{a}\right)−{f}\left({x}\right) \\ $$$$\Rightarrow\:\:{f}\left({a}−{x}\right)+{f}\left({a}\right){f}\left(\mathrm{2}{a}−{x}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:{f}\:^{\mathrm{2}} \left({a}\right){f}\left({x}−{a}\right)−{f}\left({a}+{x}\right) \\ $$$${f}\left(\mathrm{2}{a}−{x}\right)=\left[{f}\left({a}\right)−\frac{\mathrm{1}}{{f}\left({a}\right)}\right]{f}\left({x}−{a}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\frac{{f}\left({a}+{x}\right)}{{f}\left({a}\right)} \\ $$$${x}={a},\:{y}=\mathrm{0} \\ $$$${f}\left({a}\right)={f}\left({a}\right)−{f}\left({a}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:{f}\left({a}−{x}\right)=−{f}\left({a}+{x}\right) \\ $$$${now}\:\:{x}\rightarrow{x}−{a} \\ $$$$\Rightarrow\:\:{f}\left(\mathrm{2}{a}−{x}\right)=−{f}\left({x}\right)\: \\ $$$$\:\:{hence}\:\left({C}\right). \\ $$
Answered by aleks041103 last updated on 11/Aug/21
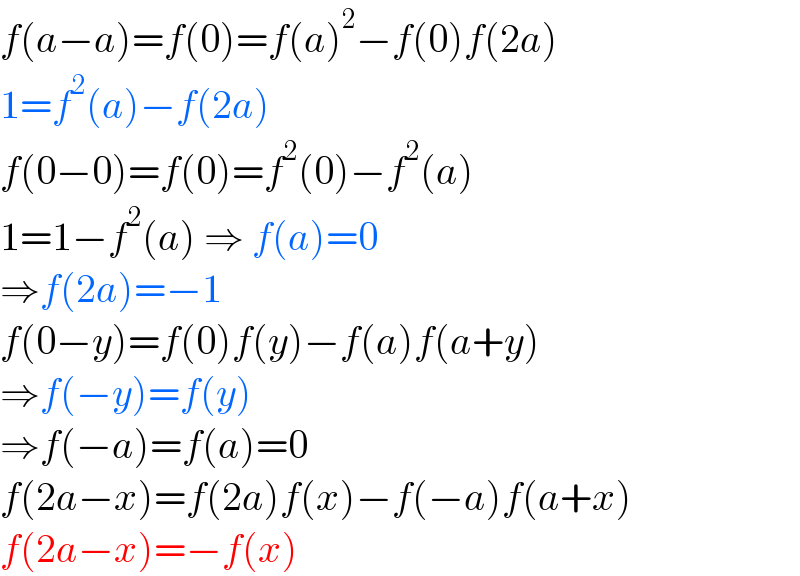
$${f}\left({a}−{a}\right)={f}\left(\mathrm{0}\right)={f}\left({a}\right)^{\mathrm{2}} −{f}\left(\mathrm{0}\right){f}\left(\mathrm{2}{a}\right) \\ $$$$\mathrm{1}={f}^{\mathrm{2}} \left({a}\right)−{f}\left(\mathrm{2}{a}\right) \\ $$$${f}\left(\mathrm{0}−\mathrm{0}\right)={f}\left(\mathrm{0}\right)={f}^{\mathrm{2}} \left(\mathrm{0}\right)−{f}^{\mathrm{2}} \left({a}\right) \\ $$$$\mathrm{1}=\mathrm{1}−{f}^{\mathrm{2}} \left({a}\right)\:\Rightarrow\:{f}\left({a}\right)=\mathrm{0} \\ $$$$\Rightarrow{f}\left(\mathrm{2}{a}\right)=−\mathrm{1} \\ $$$${f}\left(\mathrm{0}−{y}\right)={f}\left(\mathrm{0}\right){f}\left({y}\right)−{f}\left({a}\right){f}\left({a}+{y}\right) \\ $$$$\Rightarrow{f}\left(−{y}\right)={f}\left({y}\right) \\ $$$$\Rightarrow{f}\left(−{a}\right)={f}\left({a}\right)=\mathrm{0} \\ $$$${f}\left(\mathrm{2}{a}−{x}\right)={f}\left(\mathrm{2}{a}\right){f}\left({x}\right)−{f}\left(−{a}\right){f}\left({a}+{x}\right) \\ $$$${f}\left(\mathrm{2}{a}−{x}\right)=−{f}\left({x}\right) \\ $$
