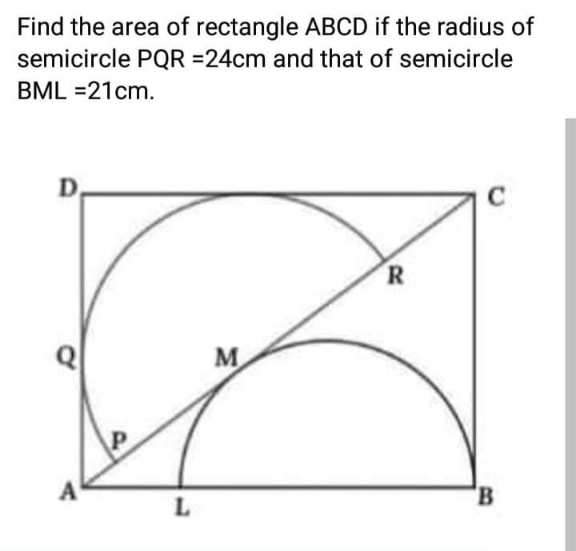
Question Number 153580 by liberty last updated on 08/Sep/21
Answered by mr W last updated on 08/Sep/21

Commented by mr W last updated on 08/Sep/21
![((a−R)/R)=(R/(b−R)) ⇒(a−R)b=aR (r/(a−r))=(b/( (√(a^2 +b^2 )))) r^2 a^2 =(a^2 −2ar)b^2 r^2 (a−R)^2 =R^2 (a^2 −2ar) ⇒(R^2 −r^2 )a^2 −2rR(R−r)a−r^2 R^2 =0 a=((rR[R−r+(√(2R(R−r)))])/(R^2 −r^2 )) b=(R/(1−(R/a)))=(R/(1−((R^2 −r^2 )/(r[R−r+(√(2R(R−r)))])))) with R=24, r=21: ⇒a=56 ⇒b=42 area=ab=2352](https://www.tinkutara.com/question/Q153648.png)
$$\frac{{a}−{R}}{{R}}=\frac{{R}}{{b}−{R}} \\ $$$$\Rightarrow\left({a}−{R}\right){b}={aR} \\ $$$$\frac{{r}}{{a}−{r}}=\frac{{b}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$${r}^{\mathrm{2}} {a}^{\mathrm{2}} =\left({a}^{\mathrm{2}} −\mathrm{2}{ar}\right){b}^{\mathrm{2}} \\ $$$${r}^{\mathrm{2}} \left({a}−{R}\right)^{\mathrm{2}} ={R}^{\mathrm{2}} \left({a}^{\mathrm{2}} −\mathrm{2}{ar}\right) \\ $$$$\Rightarrow\left({R}^{\mathrm{2}} −{r}^{\mathrm{2}} \right){a}^{\mathrm{2}} −\mathrm{2}{rR}\left({R}−{r}\right){a}−{r}^{\mathrm{2}} {R}^{\mathrm{2}} =\mathrm{0} \\ $$$${a}=\frac{{rR}\left[{R}−{r}+\sqrt{\mathrm{2}{R}\left({R}−{r}\right)}\right]}{{R}^{\mathrm{2}} −{r}^{\mathrm{2}} } \\ $$$${b}=\frac{{R}}{\mathrm{1}−\frac{{R}}{{a}}}=\frac{{R}}{\mathrm{1}−\frac{{R}^{\mathrm{2}} −{r}^{\mathrm{2}} }{{r}\left[{R}−{r}+\sqrt{\mathrm{2}{R}\left({R}−{r}\right)}\right]}} \\ $$$${with}\:{R}=\mathrm{24},\:{r}=\mathrm{21}: \\ $$$$\Rightarrow{a}=\mathrm{56} \\ $$$$\Rightarrow{b}=\mathrm{42} \\ $$$${area}={ab}=\mathrm{2352} \\ $$
Commented by Tawa11 last updated on 08/Sep/21

$$\mathrm{Weldone}\:\mathrm{sir}. \\ $$
