Menu Close

Question-15567

Tinku Tara 0 Comments
Pin




Question Number 15567 by b.e.h.i.8.3.4.1.7@gmail.com last updated on 11/Jun/17
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 11/Jun/17
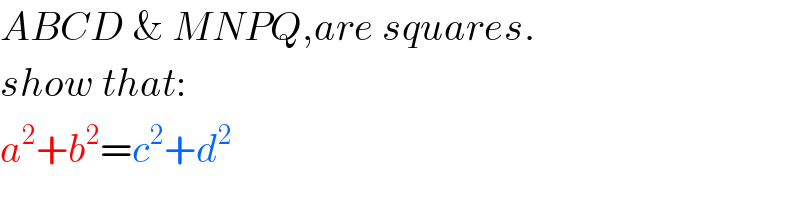
ABCD & MNPQ,are squares. show that: a^2 +b^2 =c^2 +d^2
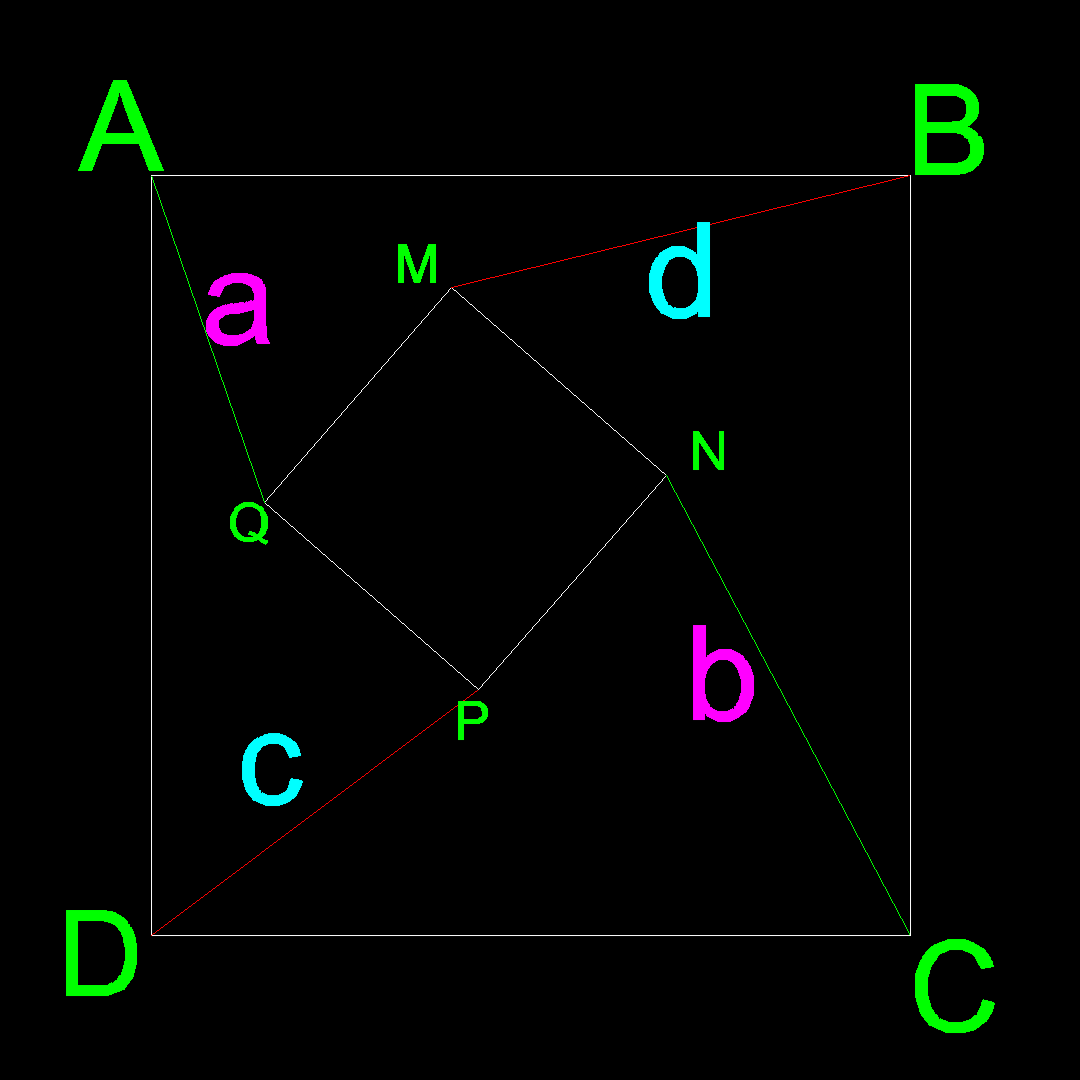
$${ABCD}\:\&\:{MNPQ},{are}\:{squares}. \\ $$$${show}\:{that}: \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} ={c}^{\mathrm{2}} +{d}^{\mathrm{2}} \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 13/Jun/17
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 13/Jun/17
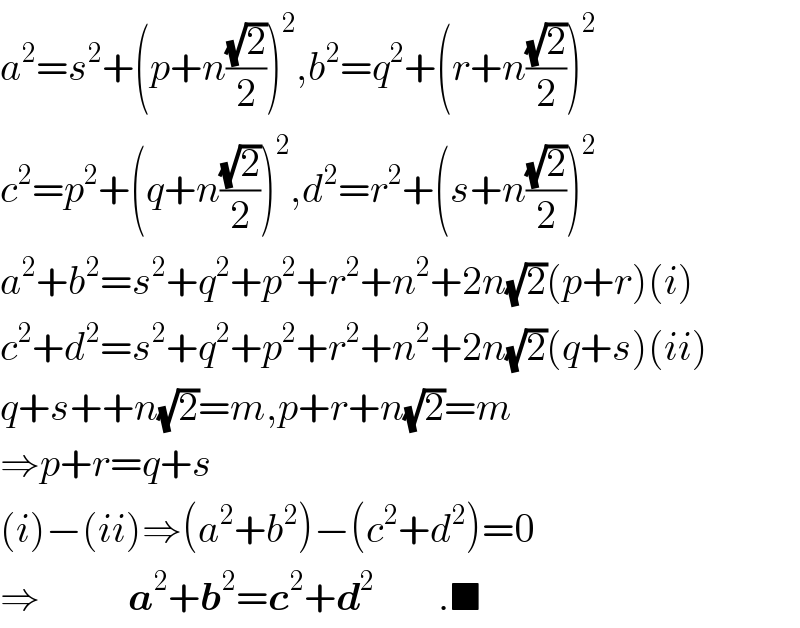
a^2 =s^2 +(p+n((√2)/2))^2 ,b^2 =q^2 +(r+n((√2)/2))^2 c^2 =p^2 +(q+n((√2)/2))^2 ,d^2 =r^2 +(s+n((√2)/2))^2 a^2 +b^2 =s^2 +q^2 +p^2 +r^2 +n^2 +2n(√2)(p+r)(i) c^2 +d^2 =s^2 +q^2 +p^2 +r^2 +n^2 +2n(√2)(q+s)(ii) q+s++n(√2)=m,p+r+n(√2)=m ⇒p+r=q+s (i)−(ii)⇒(a^2 +b^2 )−(c^2 +d^2 )=0 ⇒ a^2 +b^2 =c^2 +d^2 .■
$${a}^{\mathrm{2}} ={s}^{\mathrm{2}} +\left({p}+{n}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}} ,{b}^{\mathrm{2}} ={q}^{\mathrm{2}} +\left({r}+{n}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$${c}^{\mathrm{2}} ={p}^{\mathrm{2}} +\left({q}+{n}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}} ,{d}^{\mathrm{2}} ={r}^{\mathrm{2}} +\left({s}+{n}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} ={s}^{\mathrm{2}} +{q}^{\mathrm{2}} +{p}^{\mathrm{2}} +{r}^{\mathrm{2}} +{n}^{\mathrm{2}} +\mathrm{2}{n}\sqrt{\mathrm{2}}\left({p}+{r}\right)\left({i}\right) \\ $$$${c}^{\mathrm{2}} +{d}^{\mathrm{2}} ={s}^{\mathrm{2}} +{q}^{\mathrm{2}} +{p}^{\mathrm{2}} +{r}^{\mathrm{2}} +{n}^{\mathrm{2}} +\mathrm{2}{n}\sqrt{\mathrm{2}}\left({q}+{s}\right)\left({ii}\right) \\ $$$${q}+{s}++{n}\sqrt{\mathrm{2}}={m},{p}+{r}+{n}\sqrt{\mathrm{2}}={m} \\ $$$$\Rightarrow{p}+{r}={q}+{s} \\ $$$$\left({i}\right)−\left({ii}\right)\Rightarrow\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)−\left({c}^{\mathrm{2}} +{d}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{a}}^{\mathrm{2}} +\boldsymbol{{b}}^{\mathrm{2}} =\boldsymbol{{c}}^{\mathrm{2}} +\boldsymbol{{d}}^{\mathrm{2}} \:\:\:\:\:\:\:\:.\blacksquare \\ $$
Answered by ajfour last updated on 12/Jun/17
Commented by ajfour last updated on 12/Jun/17
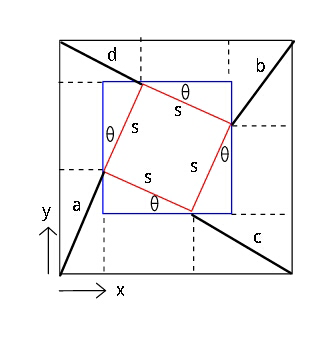
let scos θ=s_x , ssin θ=s_y l is the side of biggest square all components of lengths a, b, c, d, and s are positive. from figure above, c_x =b_x +s_y ; c_y =a_y −s_y d_x =a_x +s_y ; d_y =b_y −s_y c^2 +d^2 =c_x ^2 +c_y ^2 +d_x ^2 +d_y ^2 =(b_x +s_y )^2 +(a_y −s_y )^2 +(a_x +s_y )^2 +(b_y −s_y )^2 = (a_x ^2 +a_y ^2 )+(b_x ^2 +b_y ^2 )+4s_y ^2 +2s_y [(a_x +b_x )−(a_y +b_y )] Now (a_x +b_x )=l−(s_x +s_y ) and (a_y +b_y )=l−(s_x −s_y ) ⇒ (a_x +b_x )−(a_y +b_y )= −2s_y continuing, we have c^2 +d^2 = a^2 +b^2 +4s_y ^2 +2s_y (−2s_y ) or c^2 +d^2 = a^2 +b^2 .
$$\:{let}\:\:\:\boldsymbol{{s}}\mathrm{cos}\:\theta=\boldsymbol{{s}}_{\boldsymbol{{x}}} ,\:\:\boldsymbol{{s}}\mathrm{sin}\:\theta=\boldsymbol{{s}}_{\boldsymbol{{y}}} \\ $$$$\:\:\boldsymbol{{l}}\:{is}\:{the}\:{side}\:{of}\:{biggest}\:{square} \\ $$$${all}\:{components}\:{of}\:{lengths}\:\boldsymbol{{a}},\:\boldsymbol{{b}}, \\ $$$$\:\boldsymbol{{c}},\:\boldsymbol{{d}},\:{and}\:\boldsymbol{{s}}\:{are}\:{positive}. \\ $$$$\:\:{from}\:{figure}\:{above}, \\ $$$$\:\:\:\:\:{c}_{{x}} ={b}_{{x}} +{s}_{{y}} \:\:\:;\:\:\:{c}_{{y}} ={a}_{{y}} −{s}_{{y}} \\ $$$$\:\:\:\:\:{d}_{{x}} ={a}_{{x}} +{s}_{{y}} \:\:\:;\:\:\:{d}_{{y}} ={b}_{{y}} −{s}_{{y}} \\ $$$$\:\:\boldsymbol{{c}}^{\mathrm{2}} +\boldsymbol{{d}}^{\mathrm{2}} =\boldsymbol{{c}}_{\boldsymbol{{x}}} ^{\mathrm{2}} +\boldsymbol{{c}}_{\boldsymbol{{y}}} ^{\mathrm{2}} +\boldsymbol{{d}}_{\boldsymbol{{x}}} ^{\mathrm{2}} +\boldsymbol{{d}}_{\boldsymbol{{y}}} ^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\left(\boldsymbol{{b}}_{\boldsymbol{{x}}} +\boldsymbol{{s}}_{\boldsymbol{{y}}} \right)^{\mathrm{2}} +\left(\boldsymbol{{a}}_{\boldsymbol{{y}}} −\boldsymbol{{s}}_{\boldsymbol{{y}}} \right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:+\left(\boldsymbol{{a}}_{\boldsymbol{{x}}} +\boldsymbol{{s}}_{\boldsymbol{{y}}} \right)^{\mathrm{2}} +\left(\boldsymbol{{b}}_{\boldsymbol{{y}}} −\boldsymbol{{s}}_{\boldsymbol{{y}}} \right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:=\:\left(\boldsymbol{{a}}_{\boldsymbol{{x}}} ^{\mathrm{2}} +\boldsymbol{{a}}_{\boldsymbol{{y}}} ^{\mathrm{2}} \right)+\left(\boldsymbol{{b}}_{\boldsymbol{{x}}} ^{\mathrm{2}} +\boldsymbol{{b}}_{\boldsymbol{{y}}} ^{\mathrm{2}} \right)+\mathrm{4}\boldsymbol{{s}}_{\boldsymbol{{y}}} ^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:+\mathrm{2}\boldsymbol{{s}}_{\boldsymbol{{y}}} \left[\left(\boldsymbol{{a}}_{\boldsymbol{{x}}} +\boldsymbol{{b}}_{\boldsymbol{{x}}} \right)−\left(\boldsymbol{{a}}_{\boldsymbol{{y}}} +\boldsymbol{{b}}_{\boldsymbol{{y}}} \right)\right] \\ $$$$\:\:\:{Now}\:\:\left(\boldsymbol{{a}}_{\boldsymbol{{x}}} +\boldsymbol{{b}}_{\boldsymbol{{x}}} \right)=\boldsymbol{{l}}−\left(\boldsymbol{{s}}_{\boldsymbol{{x}}} +\boldsymbol{{s}}_{\boldsymbol{{y}}} \right) \\ $$$$\:\:{and}\:\:\:\:\:\left(\boldsymbol{{a}}_{\boldsymbol{{y}}} +\boldsymbol{{b}}_{\boldsymbol{{y}}} \right)=\boldsymbol{{l}}−\left(\boldsymbol{{s}}_{\boldsymbol{{x}}} −\boldsymbol{{s}}_{\boldsymbol{{y}}} \right) \\ $$$$\Rightarrow\:\left(\boldsymbol{{a}}_{\boldsymbol{{x}}} +\boldsymbol{{b}}_{\boldsymbol{{x}}} \right)−\left(\boldsymbol{{a}}_{\boldsymbol{{y}}} +\boldsymbol{{b}}_{\boldsymbol{{y}}} \right)=\:−\mathrm{2}\boldsymbol{{s}}_{\boldsymbol{{y}}} \\ $$$${continuing},\:{we}\:{have} \\ $$$$\:\:\:\:\:\boldsymbol{{c}}^{\mathrm{2}} +\boldsymbol{{d}}^{\mathrm{2}} \:=\:\boldsymbol{{a}}^{\mathrm{2}} +\boldsymbol{{b}}^{\mathrm{2}} +\mathrm{4}\boldsymbol{{s}}_{\boldsymbol{{y}}} ^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{2}\boldsymbol{{s}}_{\boldsymbol{{y}}} \left(−\mathrm{2}\boldsymbol{{s}}_{\boldsymbol{{y}}} \right) \\ $$$${or}\:\:\:\:\:\boldsymbol{{c}}^{\mathrm{2}} +\boldsymbol{{d}}^{\mathrm{2}} \:=\:\boldsymbol{{a}}^{\mathrm{2}} +\boldsymbol{{b}}^{\mathrm{2}} \:. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 12/Jun/17
excellent! mr Ajcour.thank you very much.
$${excellent}!\:{mr}\:{Ajcour}.{thank}\:{you}\:{very}\: \\ $$$${much}. \\ $$
Commented by ajfour last updated on 12/Jun/17
thank you sir, i shall yet look for a shorter way..
$${thank}\:{you}\:{sir},\:{i}\:{shall}\:{yet}\:{look}\:{for} \\ $$$$\:{a}\:{shorter}\:{way}.. \\ $$
Answered by ajfour last updated on 12/Jun/17
Commented by ajfour last updated on 12/Jun/17
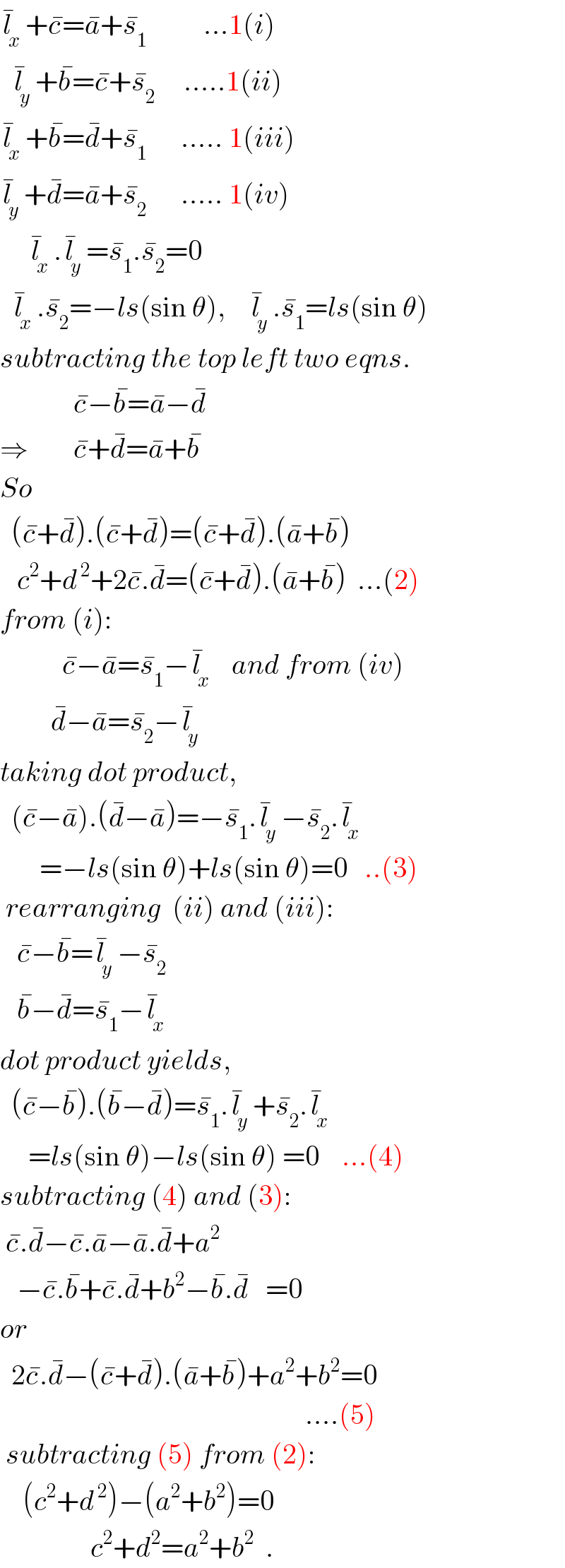
l_x ^� +c^� =a^� +s_1 ^� ...1(i) l_y ^� +b^� =c^� +s_2 ^� .....1(ii) l_x ^� +b^� =d^� +s_1 ^� ..... 1(iii) l_y ^� +d^� =a^� +s_2 ^� ..... 1(iv) l_x ^� .l_y ^� =s_1 ^� .s_2 ^� =0 l_x ^� .s_2 ^� =−ls(sin θ), l_y ^� .s_1 ^� =ls(sin θ) subtracting the top left two eqns. c^� −b^� =a^� −d^� ⇒ c^� +d^� =a^� +b^� So (c^� +d^� ).(c^� +d^� )=(c^� +d^� ).(a^� +b^� ) c^2 +d^( 2) +2c^� .d^� =(c^� +d^� ).(a^� +b^� ) ...(2) from (i): c^� −a^� =s_1 ^� −l_x ^� and from (iv) d^� −a^� =s_2 ^� −l_y ^� taking dot product, (c^� −a^� ).(d^� −a^� )=−s_1 ^� .l_y ^� −s_2 ^� .l_x ^� =−ls(sin θ)+ls(sin θ)=0 ..(3) rearranging (ii) and (iii): c^� −b^� =l_y ^� −s_2 ^� b^� −d^� =s_1 ^� −l_x ^� dot product yields, (c^� −b^� ).(b^� −d^� )=s_1 ^� .l_y ^� +s_2 ^� .l_x ^� =ls(sin θ)−ls(sin θ) =0 ...(4) subtracting (4) and (3): c^� .d^� −c^� .a^� −a^� .d^� +a^2 −c^� .b^� +c^� .d^� +b^2 −b^� .d^� =0 or 2c^� .d^� −(c^� +d^� ).(a^� +b^� )+a^2 +b^2 =0 ....(5) subtracting (5) from (2): (c^2 +d^( 2) )−(a^2 +b^2 )=0 c^2 +d^2 =a^2 +b^2 .
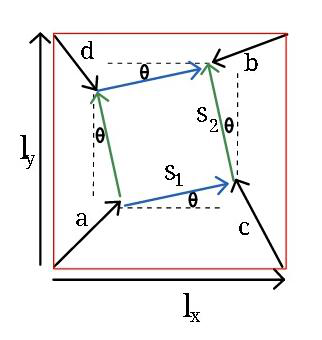
$$\bar {{l}}_{{x}} +\bar {{c}}=\bar {{a}}+\bar {{s}}_{\mathrm{1}} \:\:\:\:\:\:\:\:\:\:…\mathrm{1}\left({i}\right) \\ $$$$\:\:\bar {{l}}_{{y}} +\bar {{b}}=\bar {{c}}+\bar {{s}}_{\mathrm{2}} \:\:\:\:\:…..\mathrm{1}\left({ii}\right) \\ $$$$\bar {{l}}_{{x}} +\bar {{b}}=\bar {{d}}+\bar {{s}}_{\mathrm{1}} \:\:\:\:\:\:…..\:\mathrm{1}\left({iii}\right) \\ $$$$\bar {{l}}_{{y}} +\bar {{d}}=\bar {{a}}+\bar {{s}}_{\mathrm{2}} \:\:\:\:\:\:…..\:\mathrm{1}\left({iv}\right) \\ $$$$\:\:\:\:\:\bar {{l}}_{{x}} .\bar {{l}}_{{y}} =\bar {{s}}_{\mathrm{1}} .\bar {{s}}_{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\bar {{l}}_{{x}} .\bar {{s}}_{\mathrm{2}} =−{ls}\left(\mathrm{sin}\:\theta\right),\:\:\:\:\bar {{l}}_{{y}} .\bar {{s}}_{\mathrm{1}} ={ls}\left(\mathrm{sin}\:\theta\right) \\ $$$${subtracting}\:{the}\:{top}\:{left}\:{two}\:{eqns}. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\bar {{c}}−\bar {{b}}=\bar {{a}}−\bar {{d}} \\ $$$$\Rightarrow\:\:\:\:\:\:\:\:\bar {{c}}+\bar {{d}}=\bar {{a}}+\bar {{b}}\:\:\:\:\:\:\: \\ $$$${So} \\ $$$$\:\:\left(\bar {{c}}+\bar {{d}}\right).\left(\bar {{c}}+\bar {{d}}\right)=\left(\bar {{c}}+\bar {{d}}\right).\left(\bar {{a}}+\bar {{b}}\right) \\ $$$$\:\:\:{c}^{\mathrm{2}} +{d}^{\:\mathrm{2}} +\mathrm{2}\bar {{c}}.\bar {{d}}=\left(\bar {{c}}+\bar {{d}}\right).\left(\bar {{a}}+\bar {{b}}\right)\:\:…\left(\mathrm{2}\right) \\ $$$${from}\:\left({i}\right): \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\bar {{c}}−\bar {{a}}=\bar {{s}}_{\mathrm{1}} −\bar {{l}}_{{x}} \:\:\:{and}\:{from}\:\left({iv}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\bar {{d}}−\bar {{a}}=\bar {{s}}_{\mathrm{2}} −\bar {{l}}_{{y}} \\ $$$${taking}\:{dot}\:{product}, \\ $$$$\:\:\left(\bar {{c}}−\bar {{a}}\right).\left(\bar {{d}}−\bar {{a}}\right)=−\bar {{s}}_{\mathrm{1}} .\bar {{l}}_{{y}} −\bar {{s}}_{\mathrm{2}} .\bar {{l}}_{{x}} \\ $$$$\:\:\:\:\:\:\:=−{ls}\left(\mathrm{sin}\:\theta\right)+{ls}\left(\mathrm{sin}\:\theta\right)=\mathrm{0}\:\:\:..\left(\mathrm{3}\right) \\ $$$$\:{rearranging}\:\:\left({ii}\right)\:{and}\:\left({iii}\right): \\ $$$$\:\:\:\bar {{c}}−\bar {{b}}=\bar {{l}}_{{y}} −\bar {{s}}_{\mathrm{2}} \\ $$$$\:\:\:\bar {{b}}−\bar {{d}}=\bar {{s}}_{\mathrm{1}} −\bar {{l}}_{{x}} \\ $$$${dot}\:{product}\:{yields}, \\ $$$$\:\:\left(\bar {{c}}−\bar {{b}}\right).\left(\bar {{b}}−\bar {{d}}\right)=\bar {{s}}_{\mathrm{1}} .\bar {{l}}_{{y}} +\bar {{s}}_{\mathrm{2}} .\bar {{l}}_{{x}} \\ $$$$\:\:\:\:\:={ls}\left(\mathrm{sin}\:\theta\right)−{ls}\left(\mathrm{sin}\:\theta\right)\:=\mathrm{0}\:\:\:\:…\left(\mathrm{4}\right) \\ $$$${subtracting}\:\left(\mathrm{4}\right)\:{and}\:\left(\mathrm{3}\right): \\ $$$$\:\bar {{c}}.\bar {{d}}−\bar {{c}}.\bar {{a}}−\bar {{a}}.\bar {{d}}+{a}^{\mathrm{2}} \\ $$$$\:\:\:−\bar {{c}}.\bar {{b}}+\bar {{c}}.\bar {{d}}+{b}^{\mathrm{2}} −\bar {{b}}.\bar {{d}}\:\:\:=\mathrm{0}\:\:\: \\ $$$${or} \\ $$$$\:\:\mathrm{2}\bar {{c}}.\bar {{d}}−\left(\bar {{c}}+\bar {{d}}\right).\left(\bar {{a}}+\bar {{b}}\right)+{a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:….\left(\mathrm{5}\right) \\ $$$$\:{subtracting}\:\left(\mathrm{5}\right)\:{from}\:\left(\mathrm{2}\right): \\ $$$$\:\:\:\:\left({c}^{\mathrm{2}} +{d}^{\:\mathrm{2}} \right)−\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)=\mathrm{0}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{c}^{\mathrm{2}} +{d}^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} \:\:. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 12/Jun/17
so nice dear mr Ajfour.this proof is very beautiful. i love this.thanks.
$${so}\:{nice}\:{dear}\:{mr}\:{Ajfour}.{this}\:{proof}\:{is} \\ $$$${very}\:{beautiful}.\:{i}\:{love}\:{this}.{thanks}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *