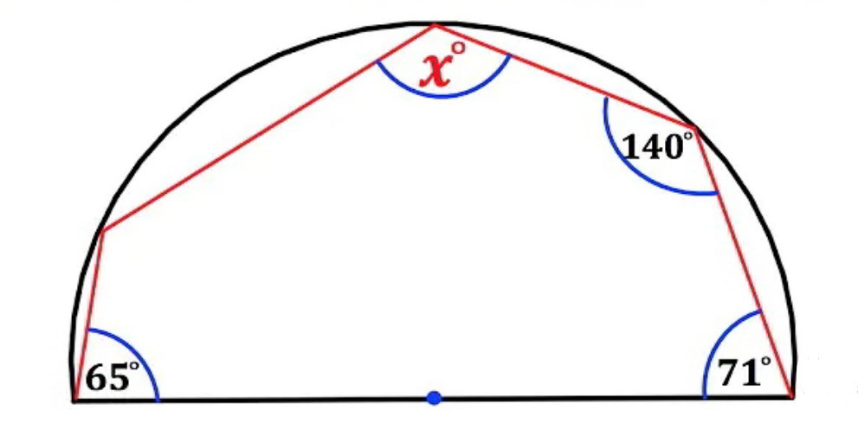
Question Number 158559 by mr W last updated on 06/Nov/21
Answered by som(math1967) last updated on 06/Nov/21
Commented by som(math1967) last updated on 06/Nov/21
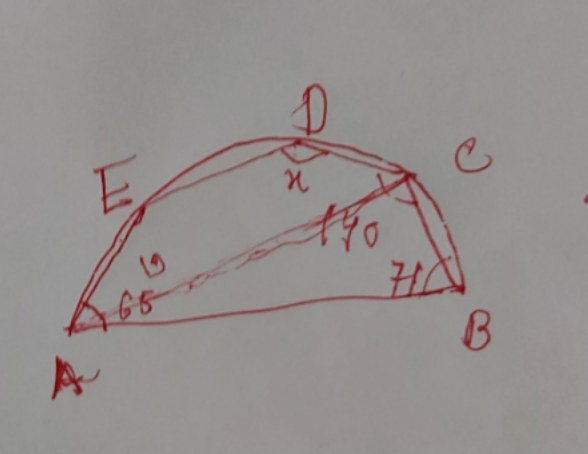
![∠ACB=90 [semicircular ] ∠BAC=90−71=19° ∴∠EAC=65−19=46° x+∠EAC=180° [ACDE cyclic] x=180−46=134° ans](https://www.tinkutara.com/question/Q158565.png)
$$\angle{ACB}=\mathrm{90}\:\:\left[{semicircular}\:\right] \\ $$$$\angle{BAC}=\mathrm{90}−\mathrm{71}=\mathrm{19}° \\ $$$$\therefore\angle{EAC}=\mathrm{65}−\mathrm{19}=\mathrm{46}°\: \\ $$$${x}+\angle{EAC}=\mathrm{180}°\:\:\left[{ACDE}\:{cyclic}\right] \\ $$$${x}=\mathrm{180}−\mathrm{46}=\mathrm{134}°\:{ans} \\ $$
Commented by mr W last updated on 06/Nov/21

$${very}\:{good}\:{sir}! \\ $$
Commented by som(math1967) last updated on 06/Nov/21
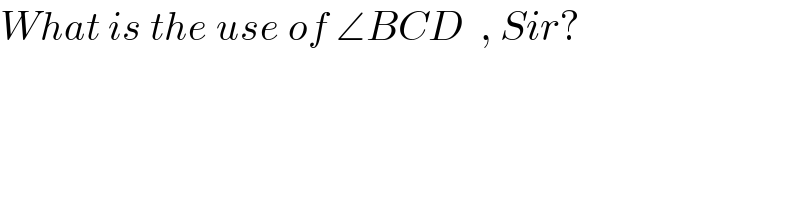
$${What}\:{is}\:{the}\:{use}\:{of}\:\angle{BCD}\:\:,\:{Sir}? \\ $$
Commented by mr W last updated on 06/Nov/21
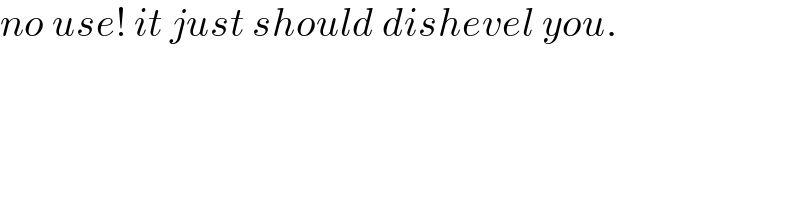
$${no}\:{use}!\:{it}\:{just}\:{should}\:{dishevel}\:{you}. \\ $$
Commented by som(math1967) last updated on 06/Nov/21
$${Ok},\:{thank}\:{you}\:{sir} \\ $$
