Question-158619

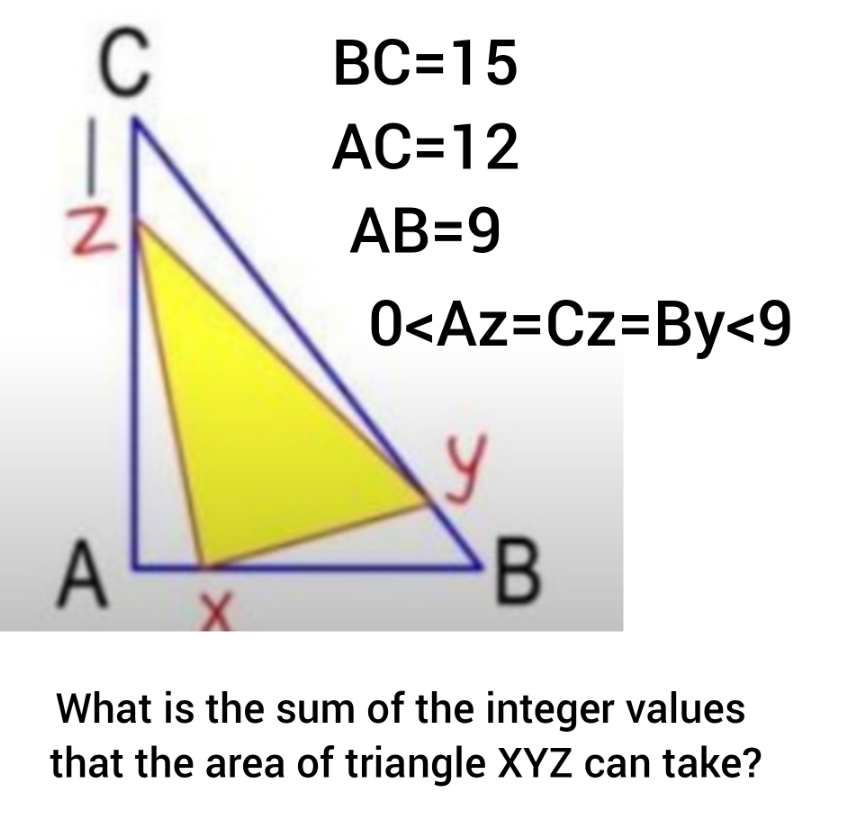
Question Number 158619 by amin96 last updated on 06/Nov/21

Commented by amin96 last updated on 06/Nov/21

$$ \\ $$

Answered by Rasheed.Sindhi last updated on 07/Nov/21

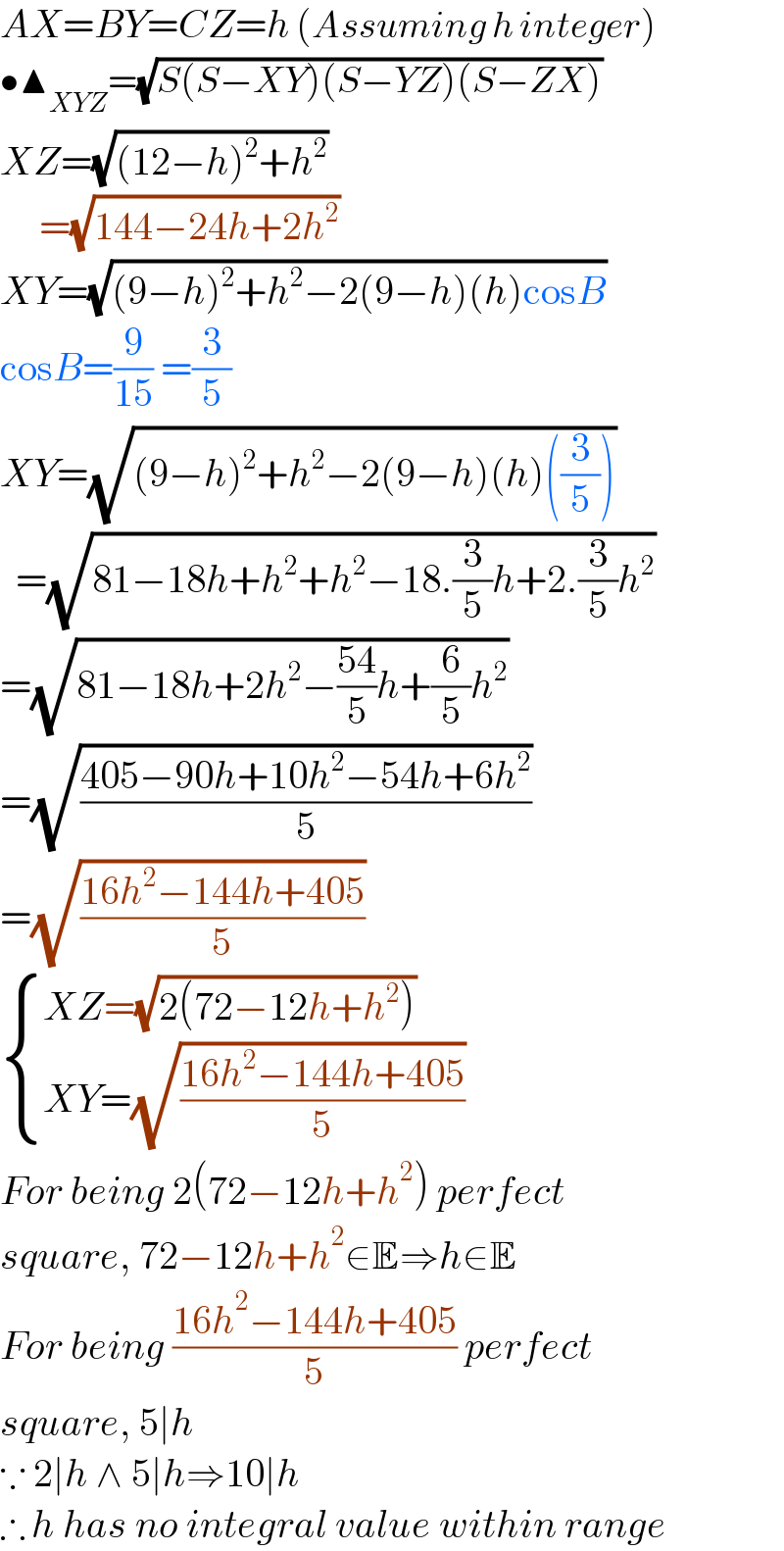
AX=BY=CZ=h (Assuming h integer) •▲_(XYZ) =(√(S(S−XY)(S−YZ)(S−ZX))) XZ=(√((12−h)^2 +h^2 )) =(√(144−24h+2h^2 )) XY=(√((9−h)^2 +h^2 −2(9−h)(h)cosB)) cosB=(9/(15)) =(3/5) XY=(√((9−h)^2 +h^2 −2(9−h)(h)((3/5)))) =(√(81−18h+h^2 +h^2 −18.(3/5)h+2.(3/5)h^2 )) =(√(81−18h+2h^2 −((54)/5)h+(6/5)h^2 )) =(√((405−90h+10h^2 −54h+6h^2 )/5)) =(√((16h^2 −144h+405)/5)) { ((XZ=(√(2(72−12h+h^2 ))))),((XY=(√((16h^2 −144h+405)/5)))) :} For being 2(72−12h+h^2 ) perfect square, 72−12h+h^2 ∈E⇒h∈E For being ((16h^2 −144h+405)/5) perfect square, 5∣h ∵ 2∣h ∧ 5∣h⇒10∣h ∴ h has no integral value within range

$${AX}={BY}={CZ}={h}\:\left({Assuming}\:{h}\:{integer}\right) \\ $$$$\bullet\blacktriangle_{{XYZ}} =\sqrt{{S}\left({S}−{XY}\right)\left({S}−{YZ}\right)\left({S}−{ZX}\right)} \\ $$$${XZ}=\sqrt{\left(\mathrm{12}−{h}\right)^{\mathrm{2}} +{h}^{\mathrm{2}} } \\ $$$$\:\:\:\:\:=\sqrt{\mathrm{144}−\mathrm{24}{h}+\mathrm{2}{h}^{\mathrm{2}} } \\ $$$${XY}=\sqrt{\left(\mathrm{9}−{h}\right)^{\mathrm{2}} +{h}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{9}−{h}\right)\left({h}\right)\mathrm{cos}{B}} \\ $$$$\mathrm{cos}{B}=\frac{\mathrm{9}}{\mathrm{15}}\:=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$${XY}=\sqrt{\left(\mathrm{9}−{h}\right)^{\mathrm{2}} +{h}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{9}−{h}\right)\left({h}\right)\left(\frac{\mathrm{3}}{\mathrm{5}}\right)} \\ $$$$\:\:=\sqrt{\mathrm{81}−\mathrm{18}{h}+{h}^{\mathrm{2}} +{h}^{\mathrm{2}} −\mathrm{18}.\frac{\mathrm{3}}{\mathrm{5}}{h}+\mathrm{2}.\frac{\mathrm{3}}{\mathrm{5}}{h}^{\mathrm{2}} } \\ $$$$=\sqrt{\mathrm{81}−\mathrm{18}{h}+\mathrm{2}{h}^{\mathrm{2}} −\frac{\mathrm{54}}{\mathrm{5}}{h}+\frac{\mathrm{6}}{\mathrm{5}}{h}^{\mathrm{2}} } \\ $$$$=\sqrt{\frac{\mathrm{405}−\mathrm{90}{h}+\mathrm{10}{h}^{\mathrm{2}} −\mathrm{54}{h}+\mathrm{6}{h}^{\mathrm{2}} }{\mathrm{5}}} \\ $$$$=\sqrt{\frac{\mathrm{16}{h}^{\mathrm{2}} −\mathrm{144}{h}+\mathrm{405}}{\mathrm{5}}} \\ $$$$\begin{cases}{{XZ}=\sqrt{\mathrm{2}\left(\mathrm{72}−\mathrm{12}{h}+{h}^{\mathrm{2}} \right)}}\\{{XY}=\sqrt{\frac{\mathrm{16}{h}^{\mathrm{2}} −\mathrm{144}{h}+\mathrm{405}}{\mathrm{5}}}}\end{cases} \\ $$$${For}\:{being}\:\mathrm{2}\left(\mathrm{72}−\mathrm{12}{h}+{h}^{\mathrm{2}} \right)\:{perfect} \\ $$$${square},\:\mathrm{72}−\mathrm{12}{h}+{h}^{\mathrm{2}} \in\mathbb{E}\Rightarrow{h}\in\mathbb{E} \\ $$$${For}\:{being}\:\frac{\mathrm{16}{h}^{\mathrm{2}} −\mathrm{144}{h}+\mathrm{405}}{\mathrm{5}}\:{perfect} \\ $$$${square},\:\mathrm{5}\mid{h} \\ $$$$\because\:\mathrm{2}\mid{h}\:\wedge\:\mathrm{5}\mid{h}\Rightarrow\mathrm{10}\mid{h} \\ $$$$\therefore\:{h}\:{has}\:{no}\:{integral}\:{value}\:{within}\:{range} \\ $$

Commented by amin96 last updated on 07/Nov/21

$$ \\ $$Is XYZ a right triangle?

Commented by Rasheed.Sindhi last updated on 07/Nov/21

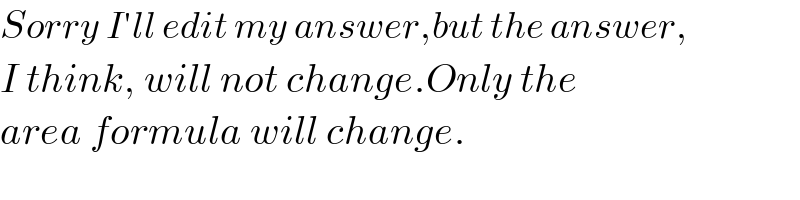
$${Sorry}\:{I}'{ll}\:{edit}\:{my}\:{answer},{but}\:{the}\:{answer}, \\ $$$${I}\:{think},\:{will}\:{not}\:{change}.{Only}\:{the} \\ $$$${area}\:{formula}\:{will}\:{change}. \\ $$

Commented by amin96 last updated on 07/Nov/21

$$ \\ $$Yes, I think so too. So there is no integer for the area of the yellow triangle?

Commented by mr W last updated on 07/Nov/21

$${only}\:{the}\:{value}\:{of}\:{the}\:{area}\:{of}\:{the}\: \\ $$$${yellow}\:{triangle}\:{should}\:{be}\:{integer},\: \\ $$$${not}\:{the}\:{side}\:{length}\:{of}\:{the}\:{triangles}!\: \\ $$

Answered by mr W last updated on 07/Nov/21

AB=p=9, AC=q=12, BC=r=15 let AX=BY=CZ=t let Δ=area of ΔABC=54 Δ_(AZX) =(t/p)×(((q−t))/q)×Δ Δ_(BXY) =(t/r)×(((p−t))/p)×Δ Δ_(CYZ) =(t/q)×(((r−t))/r)×Δ Δ_(XYZ) =[1−((t(q−t))/(pq))−((t(p−t))/(rp))−((t(r−t))/(qr))]Δ Δ_(XYZ) =(((p+q+r)t^2 −(pq+qr+rp)t+pqr)/(pqr))Δ Δ_(XYZ) =((3(4t^2 −47t+180))/(10)) Δ_(XYZ) =((3t(4t−47))/(10))+54 ((3t(4t−47))/(10)) must be an integer k. Δ_(XYZ) =k+54 12t^2 −141t=10k with k∈Z t=((141±(√(141^2 +480k)))/(24)) 141^2 +480k≥0 ⇒k≥−((141^2 )/(480)) ⇒k≥−41 such that 0<t<9 ⇒−41≤k≤−1 therefore we have following integer area for ΔXYZ: k+54 −41≤k≤−30 for each k two triangles exist. −29≤k≤−1 for each k one triangle exists. that means totally 29+2×12=43 possible yellow triangles exist. sum of all possible integer areas: 41×54+(−41−40−39−...−1) =41×54−((42×41)/2)=1335

$${AB}={p}=\mathrm{9},\:{AC}={q}=\mathrm{12},\:{BC}={r}=\mathrm{15} \\ $$$${let}\:{AX}={BY}={CZ}={t} \\ $$$${let}\:\Delta={area}\:{of}\:\Delta{ABC}=\mathrm{54} \\ $$$$\Delta_{{AZX}} =\frac{{t}}{{p}}×\frac{\left({q}−{t}\right)}{{q}}×\Delta \\ $$$$\Delta_{{BXY}} =\frac{{t}}{{r}}×\frac{\left({p}−{t}\right)}{{p}}×\Delta \\ $$$$\Delta_{{CYZ}} =\frac{{t}}{{q}}×\frac{\left({r}−{t}\right)}{{r}}×\Delta \\ $$$$\Delta_{{XYZ}} =\left[\mathrm{1}−\frac{{t}\left({q}−{t}\right)}{{pq}}−\frac{{t}\left({p}−{t}\right)}{{rp}}−\frac{{t}\left({r}−{t}\right)}{{qr}}\right]\Delta \\ $$$$\Delta_{{XYZ}} =\frac{\left({p}+{q}+{r}\right){t}^{\mathrm{2}} −\left({pq}+{qr}+{rp}\right){t}+{pqr}}{{pqr}}\Delta \\ $$$$\Delta_{{XYZ}} =\frac{\mathrm{3}\left(\mathrm{4}{t}^{\mathrm{2}} −\mathrm{47}{t}+\mathrm{180}\right)}{\mathrm{10}} \\ $$$$\Delta_{{XYZ}} =\frac{\mathrm{3}{t}\left(\mathrm{4}{t}−\mathrm{47}\right)}{\mathrm{10}}+\mathrm{54} \\ $$$$\frac{\mathrm{3}{t}\left(\mathrm{4}{t}−\mathrm{47}\right)}{\mathrm{10}}\:{must}\:{be}\:{an}\:{integer}\:{k}. \\ $$$$\Delta_{{XYZ}} ={k}+\mathrm{54} \\ $$$$\mathrm{12}{t}^{\mathrm{2}} −\mathrm{141}{t}=\mathrm{10}{k}\:{with}\:{k}\in\mathbb{Z} \\ $$$${t}=\frac{\mathrm{141}\pm\sqrt{\mathrm{141}^{\mathrm{2}} +\mathrm{480}{k}}}{\mathrm{24}} \\ $$$$\mathrm{141}^{\mathrm{2}} +\mathrm{480}{k}\geqslant\mathrm{0}\:\Rightarrow{k}\geqslant−\frac{\mathrm{141}^{\mathrm{2}} }{\mathrm{480}}\:\Rightarrow{k}\geqslant−\mathrm{41} \\ $$$${such}\:{that}\:\mathrm{0}<{t}<\mathrm{9}\:\Rightarrow−\mathrm{41}\leqslant{k}\leqslant−\mathrm{1} \\ $$$${therefore}\:{we}\:{have}\:{following} \\ $$$${integer}\:{area}\:{for}\:\Delta{XYZ}:\:{k}+\mathrm{54} \\ $$$$−\mathrm{41}\leqslant{k}\leqslant−\mathrm{30}\:{for}\:{each}\:{k}\:{two}\:{triangles}\:{exist}. \\ $$$$−\mathrm{29}\leqslant{k}\leqslant−\mathrm{1}\:{for}\:{each}\:{k}\:{one}\:{triangle}\:{exists}. \\ $$$${that}\:{means}\:{totally}\:\mathrm{29}+\mathrm{2}×\mathrm{12}=\mathrm{43}\: \\ $$$${possible}\:{yellow}\:{triangles}\:{exist}. \\ $$$${sum}\:{of}\:{all}\:{possible}\:{integer}\:{areas}: \\ $$$$\mathrm{41}×\mathrm{54}+\left(−\mathrm{41}−\mathrm{40}−\mathrm{39}−…−\mathrm{1}\right) \\ $$$$=\mathrm{41}×\mathrm{54}−\frac{\mathrm{42}×\mathrm{41}}{\mathrm{2}}=\mathrm{1335} \\ $$

Commented by mr W last updated on 07/Nov/21

an other way: max. yellow triangle should be smaller than ΔABC=54 min. yellow triangle (see Q158664) =(1−(((9×12+12×15+15×9)^2 )/(4×9×12×15×(9+12+15))))×54 ≈12.6 that means the integer value for the area of the yellow triangle can be from 13 to 53. sum of these values =(((13+53)×41)/2)=1353

$${an}\:{other}\:{way}: \\ $$$${max}.\:{yellow}\:{triangle}\:{should}\:{be}\: \\ $$$${smaller}\:{than}\:\Delta{ABC}=\mathrm{54} \\ $$$${min}.\:{yellow}\:{triangle}\:\left({see}\:{Q}\mathrm{158664}\right) \\ $$$$=\left(\mathrm{1}−\frac{\left(\mathrm{9}×\mathrm{12}+\mathrm{12}×\mathrm{15}+\mathrm{15}×\mathrm{9}\right)^{\mathrm{2}} }{\mathrm{4}×\mathrm{9}×\mathrm{12}×\mathrm{15}×\left(\mathrm{9}+\mathrm{12}+\mathrm{15}\right)}\right)×\mathrm{54} \\ $$$$\approx\mathrm{12}.\mathrm{6} \\ $$$${that}\:{means}\:{the}\:{integer}\:{value}\:{for} \\ $$$${the}\:{area}\:{of}\:{the}\:{yellow}\:{triangle}\:{can} \\ $$$${be}\:{from}\:\mathrm{13}\:{to}\:\mathrm{53}. \\ $$$${sum}\:{of}\:{these}\:{values}\: \\ $$$$=\frac{\left(\mathrm{13}+\mathrm{53}\right)×\mathrm{41}}{\mathrm{2}}=\mathrm{1353} \\ $$

Commented by Tawa11 last updated on 07/Nov/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply